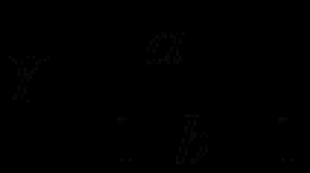Внутренняя норма доходности (англ. Internal Rate of Return, IRR ), известная также как внутренняя ставка доходности, является ставкой дисконтирования, при которой чистая приведенная стоимость (англ. Net Present Value, NPV ) проекта равна нолю. Другими словами, настоящая стоимость всех ожидаемых денежных потоков проекта равна величине первоначальных инвестиций. В основе метода IRR лежит методика дисконтированных денежных потоков, а сам показатель получил широкое использование в бюджетировании капитальных вложений и при принятии инвестиционных решений в качестве критерия отбора проектов и инвестиций.

Критерий отбора проектов

Правило принятия решений при отборе проектов можно сформулировать следующим образом:

1. Внутренняя норма доходности должна превышать средневзвешенную стоимость капитала (англ. Weighted Average Cost of Capital, WACC ), привлеченного для реализации проекта, в противном случае его следует отклонить.
2. Если несколько независимых проектов соответствуют указанному выше критерию, все они должны быть приняты. Если они являются взаимоисключающими, то принять следует тот из них, у которого наблюдается максимальный IRR.

Предположим, что существует два проекта с одинаковым уровнем риска, первоначальными инвестициями и общей суммой ожидаемых денежных потоков. Для более наглядной иллюстрации концепции стоимости денег во времени, поступление денежных потоков по Проекту А ожидается несколько раньше, чем по Проекту Б.

Подставим представленные в таблице данные в уравнение.

Для решения этих уравнений можно воспользоваться функцией «ВСД» Microsoft Excel, как это показано на рисунке ниже.

1. Выберите ячейку вывода I4 .
2. Нажмите кнопку fx , выберите категорию «Финансовые », а затем функцию «ВСД » из списка.
3. В поле «Значение » выберите диапазон данных C4:H4 , оставьте пустым поле «Предположение » и нажмите кнопку OK .

Таким образом, внутренняя ставка доходности Проекта А составляет 20,27%, а Проекта Б 12,01%. Схема дисконтированных денежных потоков представлена на рисунке ниже.

Предположим, что средневзвешенная стоимость капитала для обеих проектов составляет 9,5% (поскольку они обладают одним уровнем риска). Если они являются независимыми, то их следует принять, поскольку IRR выше WACC. Если бы они являлись взаимоисключающими, то принять следует Проект А из-за более высокого значения IRR.

Преимущества и недостатки метода IRR

Использование метода внутренней нормы доходности имеет три существенных недостатка.

1. Предположение, что все положительные чистые денежные потоки будут реинвестированы по ставке IRR проекта. В действительности такой сценарий маловероятен, особенно для проектов с ее высокими значениями.
2. Если хотя бы одно из значений ожидаемых чистых денежных потоков будет отрицательным, приведенное выше уравнение может иметь несколько корней. Эта ситуация известна как проблема множественности IRR.
3. Конфликт между методами NPV и IRR может возникнуть при оценке взаимоисключающих проектов. В этом случае у одного проекта будет более высокая чистая приведенная стоимость, но более низкая внутренняя норма доходности, а у другого наоборот. В такой ситуации следует отдавать предпочтение проекту с более высокой чистой приведенной стоимостью.

Рассмотрим конфликт NPV и IRR на следующем примере.

Для каждого проекта была рассчитана чистая приведенная стоимость для диапазона ставок дисконтирования от 1% до 30%. На основании полученных значений NPV построен следующий график.

При стоимости капитала от 1% до 13,092% реализация Проекта А является более предпочтительной, поскольку его чистая приведенная стоимость выше, чем у Проекта Б. Стоимость капитала 13,092% является точкой безразличия, поскольку оба проекта обладают одинаковой чистой приведенной стоимостью. При стоимости капитала более 13,092% предпочтительной уже является реализация Проекта Б.

С точки зрения IRR, как единственного критерия отбора, Проект Б является более предпочтительным. Однако, как можно убедиться на графике, такой вывод является ложным при стоимости капитала менее 13,092%. Таким образом, внутреннюю норму доходности целесообразно использовать в качестве дополнительного критерия отбора при оценке нескольких взаимоисключающих проектов.

IRR - это Internal Rate of Return, что переводится на русский язык как «внутренняя норма доходности». Так называется один из двух основных методов оценки инвестиционных проектов. В интернете немало статей, представляющих собой краткое изложение данной темы по учебникам финансового анализа. Их общий минус в том, что в них слишком много математики и слишком мало объяснений.

В данной статье приведены не только формула и определение IRR, но есть примеры расчетов этого показателя и интерпретации полученных результатов.

IRR - что это такое? Формула IRR.

IRR или внутренняя норма доходности - это ставка процента, при которой приведенная стоимость всех денежных потоков инвестиционного проекта (т.е. NPV) равна нулю. Это означает, что при такой ставке процента инвестор сможет возместить свою первоначальную инвестицию, но не более того. О том, как пользоваться показателем IRR для одобрения инвестиционных проектов рассказывается чуть дальше в этой статье. Для начала надо научиться рассчитывать величину внутренней нормы доходности IRR, или, как ее еще называют, внутренней нормы рентабельности.

Математика расчета IRR довольно простая. Лучше всего рассмотреть ее на элементарных примерах. Для расчета показателя в одной из более ранних статей на этом сайте были использованы проекты А и Б с одинаковой суммой первоначальной инвестиции (10,000), но с разными по величине притоками денежных средств в последующие 4 года. Удобно будет воспользоваться этими примерами и для изучения формулы расчета показателя IRR.

Приведенная (к сегодняшнему моменту) стоимость всех денежных потоков для четырехлетних проектов будет вычисляться по формуле:

где NPV - чистая приведенная стоимость, CF - денежные потоки (Cash Flows), R - % ставка, стоимость капитала, 0,1,2,3,4 — количество периодов времени от сегодняшнего момента.

Если приравнять NPV к нулю, а вместо CF подставить денежные потоки, соответствующие каждому проекту, то в уравнении останется одна переменная R. Ставка процента, которая будет решением данного уравнения, т.е. при которой сумма всех слагаемых будет равна нулю, и будет называться IRR или внутренней нормой доходности.

Для проекта А уравнение примет вид:

Для проекта Б можно написать аналогичную формулу для расчета IRR, только денежные потоки будут другими:

Чтобы было еще понятнее, можно нанести денежные потоки от проекта на шкалу времени и представить дисконтирование наглядно. Скажем, для проекта А расчет внутренней нормы доходности можно представить в таком виде:

В общем виде для любого инвестиционного проекта формула для расчета IRR выглядит так:

где CF t - денежные потоки от проекта в момент времени t , n — количество периодов времени, IRR - внутренняя норма доходности. Обратите внимание, что понятие IRR в отличие от NPV имеет смысл только для инвестиционного проекта, т.е. когда один из денежных потоков (обычно самый первый) является отрицательным. Этот отрицательный денежный поток и будет являться первоначальной инвестицией. В противном случае мы никогда не получим NPV, равную нулю.

Расчет внутренней нормы доходности с помощью программы Excel — примеры

Вручную с помощью обычного калькулятора найти значение IRR для проектов А и Б невозможно, потому что в данном случае получается уравнение 4-й степени (в нем будет множитель IRR 4 — ставка процента в четвертой степени). Проблему решения такого уравнения n-ой степени можно устранить или с помощью финансового калькулятора, или, что проще, можно воспользоваться встроенной функцией в программе Excel. Эта функция находится в разделе Формулы -> Финансовые, и называется она ВСД (внутренняя ставка доходности).

Для проекта А значение IRR, как видно из рисунка ниже, составит 14,48%.

Чтобы воспользоваться функцией ВСД, в строку «значения» нужно поставить ссылки на ячейки таблицы с суммами денежных потоков. Ячейку «предположение» можно не заполнять, этот аргумент, является необязательным. Выводимое значение 0,144888443 — это и будет искомая IRR, т.е. внутренняя норма доходности данного проекта. Если перевести эту величину в проценты, то она равна 14,48% с точностью до двух знаков после запятой.

Для проекта Б значение IRR согласно Excel равно 11,79%.

Приведу важные пояснения по этой функции из раздела «справка» с моими дополнениями:

1. Значения должны содержать по крайней мере одну положительную и одну отрицательную величину. В противном случае функция ВСД возвращает значение ошибки #ЧИСЛО!. Действительно, если нет отрицательного денежного потока, то NPV не может быть равно нулю, а в этом случае IRR не существует.
2. Для расчета функции ВСД важен порядок поступлений денежных средств. Поэтому если потоки денежных средств отличаются по величине в разные периоды, что обычно и бывает, то их необходимо внести в таблицу в соответствии со временем их возникновения.
3. В Microsoft Excel для вычисления ВСД используется метод итераций. Функцией ВСД выполняются циклические вычисления начиная со значения аргумента «предположение», пока не будет получен результат с точностью 0,00001%. В большинстве случаев для вычислений с помощью функции ВСД нет необходимости задавать аргумент «предположение». Если он опущен, предполагается значение 0,1 (10%).

Другими словами функция ВСД программы Excel будет искать значение IRR подбором, последовательно подставляя в формулу различные величины % ставки, начиная со значения в ячейке «предположение» или с 10%. Если функция ВСД не сможет получить результат после 20 попыток, выдается значение ошибки #ЧИСЛО! Поэтому в некоторых случаях, например, если вы будете считать IRR для ежемесячных потоков за несколько лет, лучше поставить в ячейку «предположение» ожидаемую вами величину ежемесячной процентной ставки. Иначе Excel может не справиться с расчетом за 20 попыток.

Графический метод расчета IRR

До появления персональных компьютеров обычно использовался графический метод определения IRR. Ниже представлены графики изменения NPV для проектов А и Б в зависимости от ставки процента. Для построения графиков нужно найти значение NPV, подставляя в формулу NPV различные значения ставки дисконтирования. можно прочитать в одной из моих предыдущих статей.

На рисунке выше синий график — проект А, красный график — проект Б. Пересечение графиков с осью X (в этой точке NPV проекта равно нулю) как раз и даст значение IRR для этих проектов. Нетрудно видеть, что графический метод дает величину IRR, аналогичную найденным в Excel значениям внутренней нормы доходности для проектов А — 14,5% и Б — 11,8%.

Как пользоваться показателем IRR для оценки инвестиционных проектов?

Любой инвестиционный проект предполагает наличие первоначальной инвестиции (оттока денежных средств), которая приведет к поступлениям денежных средств в будущем (в идеальном случае). Что же показывает внутренняя норма доходности инвестиционного проекта? Она показывает ставку кредита, при которой мы не получим убытка от нашей инвестиции, т.е. результатом всех денежных притоков и оттоков в сумме будет ноль — ни прибыли, ни убытка. В этом случае наша инвестиция в проект окупится будущими поступлениями денежных средств от проекта, но в конечном итоге мы ничего не заработаем.

Правило оценки инвестиционных проектов:

Если величина IRR проекта больше стоимости капитала для компании (т.е. WACC), то проект следует принять.

Другими словами, если ставка кредита меньше ставки инвестирования (внутренней нормы доходности проекта), то заемные деньги принесут добавочную стоимость. Потому что такой инвестиционный проект заработает больший процент дохода, чем стоимость капитала, которая необходима для первоначальной инвестиции.

Например, если вы берете кредит в банке под 14% годовых для того, чтобы вложить средства в бизнес-проект, который принесет вам 20% годовых дохода, то вы на этом проекте заработаете. Если же ваши расчеты окажутся неверны, и внутренняя норма доходности вашего проекта будет ниже 14%, то вам придется отдать банку больше денежных средств, чем вы получите от проекта. То есть вы понесете убыток.

Сам банк поступает точно так же. Он привлекает деньги от населения, скажем, под 10% годовых (ставка по депозиту), а выдает кредиты под 20% годовых (цифра взята «с потолка»). До тех пор, пока ставка по принимаемым банком депозитам будет меньше, чем ставка по выдаваемым банком кредитам, банк будет жить на эту разницу.

Рассчитав показатель IRR, мы узнаем верхний допустимый уровень стоимости заемного капитала, который предполагается инвестировать. Если стоимость капитала (по которой компания может привлечь финансовые ресурсы) выше, чем внутренняя доходность проекта (IRR), то проект принесет убытки. Если стоимость капитала для компании ниже, чем IRR проекта, то компания в каком-то смысле будет работать как банк — жить на разницу между процентными ставками банковского кредитования и рентабельности инвестиции.

Чтобы логика расчета IRR стала еще понятнее, приведу несколько примеров из жизни, с которыми может столкнуться (и сталкивается) обычный человек.

Пример 1 — срочный вклад в Сбербанке

Допустим, у вас есть в наличии 6,000,000 рублей. Прямо сейчас можно сделать срочный вклад в Сбербанк, скажем, на три года. Сумма большая, поэтому нужен самый надежный банк в России. Сбербанк в данный момент предлагает ставку для вкладов свыше 2 млн. рублей на три года в размере 9,0 % годовых без капитализации и 10,29% годовых с ежемесячной капитализацией. Что такое можно прочитать по ссылке.

Поскольку мы будем снимать проценты в конце каждого года, это будет вклад без капитализации процентов, и ставка составит 9% годовых. В конце каждого года можно будет снимать сумму, равную 6,000,000*0,09 = 540,000 рублей. В конце третьего года депозит можно будет закрыть, сняв проценты за третий год и основную сумму в размере 6 миллионов рублей.

Вклад в банке — это тоже инвестиционный проект, поскольку сначала делается первоначальная инвестиция (отрицательный денежный поток), а потом собираются денежные притоки от нашего проекта. Банковский депозит — это финансовый инструмент, и самый простой способ инвестирования, доступный для обычного человека. Раз это инвестиционный проект, то можно рассчитать его внутреннюю норму доходности. Наверное, многие уже догадались, чему она будет равна.

Внутренняя норма доходности (IRR инвестиции) в банковский депозит равна процентной ставке по этому депозиту, т.е. 9%. Если 6,000,000 рублей достались вам в наследство после уплаты налогов, то это означает, что стоимость капитала для вас равна нулю. Поэтому такой инвестиционный проект будет выгоден при любой депозитной ставке. Но взять кредит на 6 миллионов в одном банке и положить эти деньги на депозит в другой банк с прибылью не получится: ставка кредита всегда будет заведомо выше ставки инвестирования. Это принцип работы банковской системы.

Пример 2 — покупка квартиры с целью заработка на сдаче ее в аренду

Свободные денежные средства можно использовать и по-другому, а именно купить квартиру в Москве, сдавать ее в аренду три года, а в конце третьего года продать эту квартиру, чтобы вернуть основной капитал. Денежные потоки от такого проекта будут очень похожи на потоки денежных средств от срочного вклада в банке: примем, что арендная плата для простоты расчета уплачивается арендатором квартиры сразу за год в конце каждого года, а стоимость квартиры в рублях через три года останется такой же, как и сейчас. Я намеренно упрощаю ситуацию, более сложные расчеты вы сможете сделать самостоятельно.

Я выбрала в Интернете первую же попавшуюся квартиру за 6 млн. рублей на СЗ Москвы. Аренда подобной однокомнатной квартиры стоит 30,000 рублей в месяц. Налоговые последствия данных сделок для простоты не учитываются.

Итак, арендная плата за год составит 30,000*12 = 360,000 рублей. Чтобы было нагляднее, денежные потоки от обоих проектов — вклад в Сбербанке и сдача 1-комнатной квартиры в аренду на северо-западе Москвы — показаны вместе в таблице ниже:

Даже без вычисления IRR видно, что сейчас банковский депозит является более доходным вариантом. Легко доказать это, если рассчитать внутреннюю норму доходности для второго проекта — она будет ниже, чем IRR по депозиту. При сдаче данной однокомнатной московской квартиры в течение трех лет при условии ее продажи в конце третьего года IRR инвестиции составит 6,0% годовых.

Если у вас нет наследства в сумме 6 млн рублей, то брать эти деньги в кредит, чтобы сдавать квартиру в аренду неразумно, так как ставка кредитования сейчас заведомо выше, чем 6,0% внутренней доходности данного проекта. Причем IRR не зависит от количества лет сдачи квартиры в аренду — внутренняя норма доходности останется такой же, если вместо трех лет сдавать ее в аренду 10 лет или 15.

Если учесть ежегодное подорожание квартиры в результате инфляции, IRR данного проекта будет выше, Например, если в первый год (2015) рублевая стоимость квартиры вырастет на 10%, во второй (2016) на 9%, а в третий (2017) на 8%, то к концу третьего года ее можно будет продать за 6,000,000*1,10*1,09*1,08 = 7,769,520 рублей. Такое увеличение денежного потока в третий год проекта даст IRR, равную 14,53%. Поэтому если бы мы могли предсказать будущие рублевые цены на квартиры с большой точностью, то наш проект стал бы более реальным. Но все равно невыгодным в нынешней ситуации, когда ставка рефинансирования ЦБ равна 17%, и, соответственно, все банковские кредиты слишком дороги.

Расчет IRR при ежемесячных потоках денежных средств

С помощью функции ВСД можно рассчитать IRR инвестиционного проекта при равных промежутках времени между денежными потоками. Результатом вычислений будет процентная ставка за период — год, квартал, месяц. Например, если бы мы считали, что платежи за аренду квартиры приходят в конце каждого месяца (а не года), то надо было бы сделать таблицу Excel с 36-ю платежами по 30,000 рублей. В этом случае функция ВСД выдала бы значение внутренней нормы доходности проекта за месяц . Для нашего проекта IRR получилась равной 0,5% в месяц. Это соответствует годовой % ставке в размере 6,17% (рассчитывается как (1+0,005) 12 -1), что ненамного больше, чем 6,0%, рассчитанных ранее.

Если вы захотите получить этот результат самостоятельно, обязательно заполните ячейку «предположение» — поставьте туда 0,03, иначе вы получите на выходе ошибку #ЧИСЛО!, потому что Excel не хватит 20 попыток, чтобы рассчитать IRR.

Расчет IRR при неравных промежутках времени между денежными потоками

Excel предоставляет возможность рассчитать внутреннюю норму доходности проекта и в том случае, если денежные потоки от проекта поступают через неравные промежутки времени. Для расчета IRR такого проекта надо использовать функцию ЧИСТВНДОХ и в качестве аргумента указать не только ячейки с денежными потоками, но и ячейки с датами их поступлений. Например, если мы перенесем срок продажи квартиры вместе с последней арендной платой на конец четвертого года (с 31.12.17 на 31.12.18), а в конце третьего года у нас не будет поступлений денежных средств, то IRR упадет с 6% до 4,53% годовых. Обратите внимание, что рассчитать внутреннюю норму доходности в данном случае можно будет только с помощью функции ЧИСТВНДОХ, потому что фукция ВСД даст тот же результат, который и был — 6%, т.е. изменение периода времени ВСД не учтет.

«Куда идем мы с Пятачком, большой, большой секрет…»

Нынешняя ставка рефинансирования, равная 17%, убивает и бизнес, и банки. Потому что трудно найти инвестиционные проекты, которые бы окупались при таких ставках кредитования. Как развивать бизнес в подобных условиях? Торговля оружием и наркотиками, конечно, будут прибыльны и в этом случае, но большая часть бизнесов будут в лучшем случае выживать, а в худшем разорятся.

И как будут зарабатывать банки, если инвестиционных проектов с такой высокой доходностью просто не существует? А чтобы платить нам выросшие проценты по вкладам, банки должны где-то зарабатывать средства для этого.

Россия смогла бы выдержать и более низкий курс рубля по отношению к основным валютам, но справиться еще и с высокой процентной ставкой в экономике — это уже перебор.

В 2014 году мы неоднократно слышали, что ЦБ РФ занимается таргетированием инфляции. И делалось это с благими намерениями — чем ниже инфляция, тем легче добиться окупаемости инвестиций. Но получается, что хотели «как лучше», а получилось «как всегда». При дорогой валюте, как сейчас, в России могло бы успешно развиваться собственное производство, импортозамещение стало бы реальностью. Но нет, мы не ищем легких путей, а что хуже всего, мы не учимся на своих ошибках. И живем, как в том анекдоте:

«В прошлом году посеяли 100 га пшеницы. Все поел хомяк…В этом году собираемся засеять 200 га пшеницы. Нехай хомяк подавится!»

Внутренняя норма рентабельности (IRR)

Под внутренней нормой рентабельности, или внутренней нормой прибыли (IRR) инвестиций понимают значение ставки дисконтирования, при котором NPV проекта равна нулю:

IRR = i , при котором NPV = f (i ) = 0.

Смысл расчета этого коэффициента при анализе эффективности планируемых инвестиций заключается в следующем. IRR показывает максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом. Например, если проект полностью финансируется за счет ссуды коммерческого банка, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.

На практике любое предприятие финансирует свою деятельность из различных источников. В качестве платы за пользование авансированными в деятельность предприятия финансовыми ресурсами оно уплачивает проценты, дивиденды, вознаграждения, т.е. несет некоторые обоснованные расходы на поддержание своего экономического потенциала. Показатель, характеризующий относительный уровень этих доходов, можно назвать ценой (привлечения) капитала (capital cost, СС). Этот показатель отражает сложившийся на предприятии минимум возврата на вложенный в его деятельность капитал, его рентабельность и рассчитывается по формуле средней арифметической взвешенной.

Экономический смысл этого показателя заключается в следующем: предприятие может принимать любые решения инвестиционного характера, уровень рентабельности которых не ниже текущего значения показателя СС (цены капитала для данного проекта). Именно с ним сравнивается показатель IRR, рассчитанный для конкретного проекта, при этом связь между ними такова:

• если IRR > СС, то проект следует принять;
• если IRR то проект следует отвергнуть;
• если IRR = СС, то проект ни прибыльный, ни убыточный.

Еще один вариант интерпретации состоит в трактовке внутренней нормы прибыли как возможной нормы дисконта, при которой проект еще выгоден по критерию NPV. Решение принимается на основе сравнения IRR с нормативной рентабельностью; при этом чем выше значения внутренней нормы доходности и больше разница между ее значением и выбранной ставкой дисконта, тем больший запас прочности имеет проект. Данный критерий является основным ориентиром при принятии инвестиционного решения инвестором, что вовсе не умаляет роли других критериев. Для расчета IRR с помощью таблиц дисконтирования выбираются два значения коэффициента дисконтирования таким образом, чтобы в интервале () функция меняла свое значение с "+" на "–" или с "–" на "+". Далее применяют формулу:

(5.2)

где – значение коэффициента дисконтирования, при котором ; – значение коэффициента дисконтирования, при котором .

Точность вычислений обратно пропорциональна длине интервала (), а наилучшая аппроксимация достигается в случае, когдаи– ближайшие друг к другу значения коэффициента дисконтирования, удовлетворяющие сформулированным выше условиям.

Точный расчет величины IRR возможен только при помощи компьютера.

Пример

Требуется определить значение показателя IRR для проекта, рассчитанного на три года, требующего инвестиций в размере 2000 ден. ед. и имеющего предполагаемые денежные поступления в размере 1000, 1500 и 2000 ден. ед.

Для расчета IRR с помощью таблиц дисконтирования выбираем два произвольных коэффициента дисконтирования, например, и рассчитываем значение функции NPV = Получаем NPV =f (40%) = 207 и NPV = f (50%) = -75. Таким образом, функция NPV =f (i ) меняет свое значение с "+" на "-", и данный интервал значений нас устраивает для расчета IRR (конечно, не всегда сразу удается подобрать такой интервал, иногда необходимо провести несколько итераций).

Далее, таким же образом мы можем уточнить полученное значение IRR путем нескольких итераций, определив ближайшие целые значения коэффициента дисконтирования, при которых NPV меняет знак. Для нашего примера такими целыми значениями являются значения .

Таким образом, искомое значение IRR составляет, по нашим расчетам, 47,17%. (Значение IRR, полученное с помощью финансового калькулятора, составляет 47,15%).

Основные расчеты представлены в табл. 5.5.

Таблица 5.5. Расчеты к примеру

	Инвестиции

К достоинствам этого критерия можно отнести объективность, независимость от абсолютного размера инвестиций, информативность. Кроме того, он легко может быть приспособлен для сравнения проектов с различными уровнями риска: проекты с большим уровнем риска должны иметь большую внутреннюю норму доходности. Однако у него есть и недостатки: сложность бескомпьютерных расчетов, большая зависимость от точности оценки будущих денежных потоков, а также невозможность использования в случае наличия нескольких корней уравнения.

Для определения внутренней нормы рентабельности, как и в методе чистой текущей стоимости, необходимо наличие допущений, которые в значительной степени совпадают друг с другом у обоих методов. Исключением является допущение относительно вложения высвобождающихся финансовых средств (условие реинвестирования), а также относительно различий в затратах капитала и сроке эксплуатации. Соответствующее допущение метода определения внутренней ставки (вложение по внутренней процентной ставке), как правило, не представляется целесообразным. Поэтому метод определения внутренней нормы рентабельности без учета конкретных резервных инвестиций или другой модификации условий не следует применять для оценки абсолютной выгодности, если имеют место комплексные инвестиции и тем самым происходит процесс реинвестирования. При этом типе инвестиций возникает также проблема существования нескольких корней при решении исходного уравнения. В этих случаях могут возникнуть сложности интерпретации результатов метода определения внутренней нормы рентабельности.

Метод определения внутренней нормы рентабельности для оценки относительной выгодности не следует применять, как отмечено выше, путем сравнения внутренних процентных ставок отдельных объектов. Вместо этого необходимо проанализировать инвестиции для определения разницы. В случае изолированно осуществляемых инвестиций можно сравнить внутреннюю процентную ставку с расчетной, чтобы сделать возможным сравнение выгодности. Если инвестиции для сравнения выгодности имеют комплексный характер, то применение метода определения рентабельности является нецелесообразным.

Преимущество метода внутренней нормы рентабельности в сравнении с методом чистой текущей стоимости заключается в возможности его интерпретирования. IRR характеризует начисление процентов на затраченный капитал (рентабельность затраченного капитала).

Кроме этого, внутреннюю процентную ставку можно рассматривать в качестве критической процентной ставки для определения абсолютной выгодности инвестиционной альтернативы в случае, если применяется метод чистой текущей стоимости при недейственности допущения о "надежных данных".

Таким образом, оценка инвестиций с помощью данного метода основана на определении максимальной величины ставки дисконтирования, при которой проекты останутся безубыточными.

Критерии NPV, IRR и Р/, наиболее часто применяемые в инвестиционном анализе, являются фактически разными версиями одной и той же концепции, и поэтому их результаты связаны друг с другом. Таким образом, можно ожидать выполнения следующих математических соотношений для одного проекта:

	NPV > 0		IRR > СС (0	Р1> 1
	NPV < 0		IRR < СС (0	Р1< 1
			IRR = СС (0

Существуют методики, которые корректируют метод IRR для применения в той или иной нестандартной ситуации. К одной из таких методик можно отнести метод модифицированной внутренней нормы прибыли (MIRR).

В наших размышлениях мы уже неоднократно обращали внимание, что оценивать эффективность проектов возможно только комплексно, применяя ряд специальных инструментов, среди которых группа показателей NPV, PI, PP, IRR, MIRR занимают ведущее место. В настоящей статье предлагаю вам разобрать такой показатель, как внутренняя норма доходности, который способен нивелировать некоторые недостатки чистого дисконтированного дохода и раскрыть совершенно иную грань доходности инвестиций, которая априори задается потоками наличности в результате проекта.

Что диктует генерация CF проекта?

У показателя NPV имеется особое свойство. Метод его расчета в значительной степени зависит от позиции инвестора относительно нормы прибыльности, а она часто бывает субъективна. Дело в том, что адекватно установить норму доходности вложений исключительно расчетным путем практически невозможно. Чем больше продолжительность мероприятия, тем сильнее искажение из-за закравшейся логической ошибки во время расчета ставки дисконтирования. Влияние неточности и субъективной оценки можно минимизировать, если применить иной подход, который реализуется в методе IRR инвестиционного проекта. В литературе данный показатель имеет ряд интерпретаций, поэтому обозначим его основные наименования:

• IRR или Internal Rate of Return;
• внутренняя норма доходности или ВНД;
• внутренняя норма рентабельности или ВНР.

Рассмотрим предметно данный метод. Дело в том, что расчет пошагового оборота наличности, формируемого реализацией инвестиционной задачи, уже несет в себе определенный потенциал прибыли, отображаемый в Net Cash Flow. С другой стороны, чем больше инвестор формирует требований к эффективности своих вложений, стремясь к ожидаемой прибыли, тем на меньшую величину NPV он обрекает проект. В какой-то момент чистая приведенная стоимость достигает нуля (посмотрите на представленный ниже график).

График зависимости NPV от нормы дохода проекта

Внутренняя норма рентабельности показывает нам уровень доходности инвестиционных вложений, формируемый проектом, для которого происходит покрытие всех проектных расходов за счет получаемых доходов. Данный показатель достаточно информативен, он определяет потерю ценности предстоящих приходов ДС. Норма доходности (рентабельности) называется внутренней, потому что обусловлена внутренними свойствами проекта, сложившимися пропорциями затрат и результатов.

Таким образом, генерация денежных потоков проекта определяет свою собственную логику доходности. Внутренняя норма доходности характеризует такое состояние уровня капитализации доходов (прибыли), которое закладывается еще в прогнозах выбытий и поступлений по шагам проекта на протяжении всей реализации мероприятия. Если принять, что данные планы движения ДС будут реализованы, то проявится некая внутренняя стоимость инвестиционного капитала, под которой и подразумевается ВНД.

Расчет показателя IRR

Метод ВНД предполагает равенство дисконтированных денежных потоков по искомому значению ставки дисконтирования и размера производимых инвестиций. Математически расчет значения IRR без подручных средств представляет определенные сложности. Однако современные прикладные программные продукты, такие как MS Excel, имеют в составе инструментов интегрированную функцию расчета ВНД. Следуя обоснованной выше логике, формула показателя выводится из ряда математических выражений, в первом из которых принято считать, что инвестиции осуществлены одномоментно на старте проекта.

Исходный вид выражения, предшествующего выводу формулы IRR

Формула, мягко говоря, нетривиальна. Как мы с вами видим, на первый взгляд, решение уравнения относительно IRR возможно, применяя метод последовательно реализуемых итераций, попросту, методом подбора. Внутренняя норма доходности соответствует ставке r, для которой NPV равна нулю. Исходя из предложенного определения, ВНД может быть рассмотрено как результат исчисления положительного корня уравнения, продемонстрированного выше.

Тем не менее, применяя для дисконтирующих аргументов табулированные значения, считать IRR можно, построив специальную математическую модель расчета. Для этого необходимо выбрать условный интервал в пределах значений r1 и r2, между которыми функция NPV меняет знак. Благодаря настоящему допущению внутренняя норма доходности как очередной показатель эффективности проекта рассчитывается не эмпирически, а уже математически, и формула IRR приобретает следующий вид.

Вид формулы IRR

Метод ВНД помимо достоинств имеет и ряд недостатков, среди которых можно выделить следующее.

1. Безразличие ставки IRR к последовательности поступлений и выбытия денежных средств. Как пример, заимствование или кредитование средств могут давать одинаковый результат ВНД.
2. Внутренняя норма рентабельности может иметь несколько решений в случае неоднократного изменения знака CF.
3. Вероятность ошибки результатов IRR при рассмотрении взаимоисключающих друг друга проектов. Метод предполагает допущение о тождественности альтернативных издержек для потоков наличности на протяжении всей реализации задачи, что может привести к существенным искажениям.

Примеры расчета ВНД

Рассмотрим пример вычисления показателя IRR с использованием MS Excel 2010. Будем считать, что инвестор вкладывает в строительство объекта круглую сумму в 100 млн. рублей. В результате вложений его интересует размер прибыли, соответствующий норме доходности в 10%. Реализация мероприятия запланирована на 7 лет, для каждого шага вычислены значения чистых денежных потоков, которые далее представлены в табличной форме.

Пример расчета ВНД инвестиционного проекта на основе формул MS Excel 2010

Используя встроенные функции в категории «Финансовые», мы можем рассчитать значения NPV (функция «ЧПС») и IRR (функции «ЧИСТВНДОХ» или «ВСД»). Поскольку периоды шагов по продолжительности равны, мы можем применить функцию «ВСД». Диалоговое окно Мастера функций программы Excel показано ниже. Таким образом, мы получаем возможность автоматически вычислять показатель «Внутренняя норма доходности», который для нашего примера составил значение – 29%.

Диалоговое окно Мастера функций Excel для выбора ВСД

Что же делать, если подобного инструмента расчета IRR у нас под рукой нет? Есть возможность приблизительно вывести значение показателя, используя метод визуализации. Возьмем тот же пример и построим соответствующую графическую модель. Сделаем предположение, что инвестор рассматривает три варианта нормы прибыли (доходности), которым соответствуют ставки дисконтирования в 10, 20 и 30%. Выполним расчет NPV для каждого варианта и построим график зависимости значения NPV от r по трем точкам. Точка пересечения графика оси Х соответствует значению IRR, которое примерно равно 0,29.

Способ определения IRR методом построения визуальной модели

В настоящей статье мы разобрали важный показатель из состава основных параметров эффективности уникальной инвестиционной задачи. Внутренняя норма доходности имеет простое правило для оценки проекта, по которому IRR должно быть, как минимум, выше, чем текущая кредитная ставка. В завершение хочу еще раз напомнить о том, что качественный отбор проектов возможен только при комплексном подходе в рассмотрении показателей эффективности и других оценочных инструментов.

Инвестирование – один из интересных способов заработка средств, который заключается в покупке выгодных (по мнению инвестора) активов перспективных компаний и проектов. В мире, который построен на современных рыночных (капиталистических) правилах игры, именно этот процесс является одной из его двигающих сил.

Но как определить, что тот или иной проект действительно выгоден и принесет доход? Стопроцентной гарантии никто никогда дать не может – это обратная сторона медали такого способа заработка. Тем не менее, расчет рисков для той или иной ценной бумаги (или облигации) возможно легко произвести вычисление, что минимизирует вероятность невыгодной покупки.

Дорогие читатели! Статья рассказывает о типовых способах решения юридических вопросов, но каждый случай индивидуален. Если вы хотите узнать, как решить именно Вашу проблему - обращайтесь к консультанту:

ЗАЯВКИ И ЗВОНКИ ПРИНИМАЮТСЯ КРУГЛОСУТОЧНО и БЕЗ ВЫХОДНЫХ ДНЕЙ .

Это быстро и БЕСПЛАТНО !

Именно для этих целей и была создана формула расчета ВНД (англ. IRR – «Internal rate of return»). Она включает в себя ключевые финансовые показатели акции или ценной бумаги и является действительно удобным способом рассчитать убыточность (или доходность).

Оценка рисков таким образом является простой и доступной даже тем, кто не слишком знаком с математическим анализом и экономикой, а полученный коэффициент легко анализируется и читается. Как итог: при знании нюансов и соблюдении ряда правил получаем работающий метод для оценки рисков при инвестировании.

Определение понятия и цели расчета IRR

Внутренняя норма доходности (ВНД или IRR) – ключевой критерий анализа любого доступного для инвестирования проекта. Фактически, эта величина позволяет определить минимальную ставку дисконта, при которой дисконтированные доходы от акции, опциона или ценной бумаги находятся в состоянии равенства с суммой вложения.

Фактически, определение ВНД базируется на уравнении, в котором чистая текущая стоимость (рентабельность) является нулевой. При поиске информации об IRR часто можно наткнуться на схожие термины и его варианты: внутренняя норма доходности, внутренняя ставка доходности, внутренняя ставка отдачи, норма рентабельности или норма возврата инвестиций. Проблемы с адаптацией термина привели даже к ряду сложностей при поиске информации о расчетах.

Уравнение ВНД отражает ту ситуацию, когда инвестиционный проект отдает вложившему в него средства не только инвестиционных средств, но и первоначальных вложений в ценные бумаги. Фактически, в нем рассматривается случай, когда соотношение вложенных средств к доходу является равным. Если финансовые показатели проекта приводят инвестора к каноничному уравнению IRR – это значит, что проект принесет столько же денег, сколько на него было потрачено.

Что можно получить от расчета ВНД? Ответ на вопрос о целесообразности вложений куда-либо. Фактически, уравнение позволяет узнать, какой объем вложенных средств сможет вывести проект «в ноль» и не сделать его убыточным. Подгоняя показатели под каноничную форму уравнения, инвестор может легко сравнить значение необходимого капитала с реально доступным ему и принять решение о вложении или отказе от него.

Подобранная ставка, увеличивающая денежный поток, дает возможность прийти к состоянию равновесия в расчетах. Если полученный таким образом показатель ВНД выше ставки прибыли за вложенные средства – инвестиция может быть произведена. Если ниже – проект однозначно не стоит инвестиций.

Формула расчета инвестиционного проекта

Внутренняя норма доходности рассчитывается по следующей формуле:

Другой вид формулы (с теми же обозначениями) выглядит так:

Расчет в Excel

Найти полследовательность арифметических действий, позволяющую вычислять ВНД в Microsoft Office Excel, не представляется возможным. Причина в том, что для полноценного вычисления показателей программой ей придется составить и решить уравнение четвертого порядка – такими функциями данный софт не обладает.

Благо, есть более простой способ: Excel обладает колоссальным запасом встроенных функций, среди которых нашлось место и ВСД (внутренняя ставка доходности). Достаточно лишь пройти в подменю «Финансовые» основной вкладки «Формулы» и выбрать соответствующий пункт в выпадающем списке.

Затем выстраиваем в один из столбцов доходность инвестиции, выделяем их (или прописываем в меню «Значения» при добавлении функции). Результат можно увидеть либо во всплывающем окне (графа «Значение» внизу), либо вывести ее на отдельную ячейку и изменять показатели, просчитывая каждое условие отдельно.

Ответ будет получен при определенных условиях:

• когда в перечне данных имеется хотя бы одно отрицательное число (при отсутствии отрицательного денежного потока IRR даже теоретически не может равняться 0);
• при правильном порядке указания поступлений (сначала первый год (месяц, квартал), потом второй, третий и так далее);
• если не введены данные в поле «Предположение» – это может повлиять на вычисление, производимое методом итераций (подбора).

Графический метод определения ВНД

Основное преимущество использования графического метода заключается в наглядности и простоте: достаточно просто построить таблицу и на ее основании (на компьютере или даже вручную) создать график зависимости.

В таблицу необходимо внести периоды, а также данные по денежным потокам проекта (или даже нескольких). Наиболее удобно делать это в том же табличном процессоре Excel. Дисконтировать по разным процентным ставкам (например, 5, 10 и 15%) и затем подобрать показатель более точно можно по приведенному в статье аналитическому алгоритму.

Далее на простроенных графиках ищем нулевую ось (где NPV = 0) и смотрим, какой ставке соответствует проект. Большой плюс метода – возможность наглядно сравнить инвестиционный потенциал сразу нескольких опций одновременно.

Практическое применение коэффициента

Любая инвестиция предполагает расставание с определенной суммой денежных средств, которые в теории должны дать уже прибыль (положительную разницу дохода с расходом). Показатель IRR дает ценную информацию: кредитную ставку, при которой инвестиция не окажется убыточной. При составлении уравнения определяются условия, когда проект не будет ни прибыльным, ни убыточным.

Далее все предельно просто: в случае, если показатель ВНД больше, чем общая итоговая цена капитала – проект стоит рассмотреть для инвестирования. Если нет – он даже теоретически не может быть рентабельным: в таком случае взятые в заем (кредит) средства смогут дать добавочную стоимость при вложении.

Именно по такой схеме и работают банки, проводя операции только с положительным IRR: достаточно сравнить ставки по депозитам (не более 15%) со процентами по выдаваемым в долг деньгам (не менее 20%). Разница же и составит прибыль от деятельности банка (в нашем случае), да и любого инвестиционного проекта в целом. Именно ВНД дает понять, каков максимальный порог возможного займа, который можно вложить в ценные бумаги, компанию и так далее.

Примеры

Пример первый – простейшие практические расчеты при имеющихся базовых показателях. Расчет нормы доходности при неизменной барьерной ставке. Объем вложенных средств равняется 30000$.

Доходы:

Период 1	10000$
Период 2	12000$
Период 3	11000$
Период 4	10500$

Показатель эффективной барьерной ставки — 10%.

Можно произвести вычисления без привлечения софта. Берем стандартный способ подходящего приближения, который часто используется в таких случаях.

Подбираем барьерные ставки приближенно, дабы «окружить» минимальные абсолютные значения NPV, и после осуществляем приближение. Этот метод подразумевает несколько расчетов IRR.

В крайних ситуациях можно построить функцию NPV(r)), но об этом – в разделе ниже.

Произведем вычисления барьерной ставки для r a =10,0%.

Теперь пересчитаем денежные потоки в виде нынешних стоимостей:

За первый период	PV 1 = 10000 / (1 + 0,1)^1 = 9090
За второй период	PV 2 = 12000 / (1 + 0,1)^2 = 9917
За третий	PV 3 = 11000 / (1 + 0,1)^3 = 8264
За четвертый	PV 4 = 10500 / (1 + 0,1)^4 = 7171

Итого, чистая текущая стоимость при ставке 10% (или 0,1) составляет:

NPV = (9090 + 9917 + 8264 + 7171) — 40000 = 4442$.

Теперь попробуем сделать то же, но для ставки в 15%.

Пересчитаем денежные потоки в образ нынешних стоимостей:

• PV 1 = 10000 / (1 + 0,15)^1 = 8695;
• PV 2 = 12000 / (1 + 0,15)^2 = 9073;
• PV 3 = 11000 / (1 + 0,15)^3 = 7232;
• PV 4 = 10500 / (1 + 0,15)^4 = 6003.

Для этой процентной ставки NPV вычисляется аналогично:

NPV = (8685 + 9073 + 7232+6003) — 35000 = — 4007$

Используем формулу приближения и получаем процент:

IRR = r a + (r b — r a) * NPV a /(NPV a — NPV b) = 10 + (15 — 10)*4442 / (4442 — (- 4007)) = 12,6%

Равенство справедливо, если r a < IRR < r b и NPV a > 0 > NPV b .

Ответ: полученный показатель окупаемости инвестиции составляет 12,6%, что выше заданной вначале эффективной барьерной ставки в 10%. Вывод: проект достоин рассмотрения и может стать рентабельным.

Тем не менее, подобный алгоритм не работает в тех случаях, когда внутреннюю норму доходности необходимо находить при изменяющейся барьерной ставке.

Дано:

Условие то же, что и в прошлом примере: вычислить вероятность окупаемости проекта и целесообразность инвестирования в него. Рассчитаем для ставки дисконтирования одинаковой r a =20,0%

Подсчитываем внутреннюю норму, как и в предыдущем примере:

NPV = (6666 + 4513 + 4050) — 15000 = 229$

Теперь сделаем те же вычисления для r b = 25,0%

Пересчитаем денежные потоки в вид текущих стоимостей:

Первый отрезок времени	PV 1 = 8000 / (1 + 0,25)^1 = 6400$
Второй отрезок времени	PV 2 = 6500 / (1 + 0,25)^2 = 4160$
Третий отрезок времени	PV 3 = 7000 / (1 + 0,25)^3 = 3584$

И все та же норма по аналогии:

NPV = (6400 + 4160 + 3584) — 15000 = — 864$

Итоговый показатель составит:

IRR = 20 + (25 — 20)*229 / (229 — (- 864)) = 21%

Так как показатель барьерной ставки изменяется, то сопоставление необходимо сделать именно с показателем внутренней барьерной ставки. В соответствии с расчетом образца эффективная барьерная ставка составит 10,895%. Вывод таков: полученный окупаемости равен 21%, что значительно выше имеющихся средних 11%. Можно смело инвестировать в проект.

Ценное замечание: правило, согласно которому выбирается проект с большим показателем внутренней нормы доходности, действует лишь в общих случаях. Оценка может изменяться кардинально, если учесть реинвестиции. В таком случае показателя барьерной ставки недостаточно проект с меньшим IRR, может быть выгоднее проекта с большими цифрами.

Модифицированная ВНД (MIRR)

Как уже говорилось выше, ВНД учитывает лишь те ситуации, в которых осуществляется первичное инвестирование. В случаях, когда происходит повторное вложение средств, он не работает: полученные по расчетам результаты могут прямо противоречить целесообразности вложения средств. Для облегчения задачи именно в этих ситуациях была создана модифицированная ВНД (или MIRR).

Формула для ее определения выглядит подобным образом, только учитывает ставку реинвестирования:

К слову, в Excel имеется и эта функция – она находится в том же списке под названием «МВСД».

Недостатки использование данного метода

Существует ряд существенных недостатков, которые могут оттолкнуть инвестора от использования вычислений на базе IRR:

• относительная громоздкость расчетов в случае большого количества отрезков времени;
• необходимость получения полных и актуальных данных о движении капитала в предприятии – чистая прибыль может отличаться от имеющейся в расчетах;
• графический способ позволяет визуально оценить необходимую величину процентной ставки, но дает лишь приблизительные результаты.

Ограничения и недостатки внутренней нормы доходности

Существует сразу несколько ограничений, которые накладывает на инвестора использование ВНД или МВНД:

• трудно прогнозировать движение денежных средств в будущем – многие факторы формула попросту не учитывает;
• с помощью IRR и MIRR не представляется возможным вычислить дисконтированный объем средств для вложения;
• если брать за основу разные периоды или иметь дело с произвольным чередованием прибыли и убытков – можно получить сразу несколько отличных друг от друга показателей ВНД, что способно запутать при принятии решения;
• стандартная формула ВНД никак не может описать процесс реинвестирования и способна выдавать в этом случае прямо противоречащие реальному положению дел результаты.

ВНД (или IRR) – один из значимых экономических показателей, который подойдет для предварительной оценки потенциала определенного вложения. Метод имеет как преимущества, так и недостатки, но все же среди простых и доступных достоит занять свое заслуженное место. Ключевой плюс – возможность выполнить расчеты четырьмя разными способами (аналитически, графически и посредством табличного процессора).