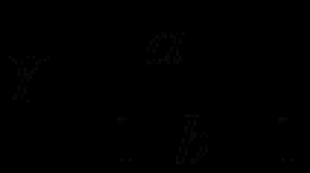Временная стоимость или, как ещё часто говорят, временная оценка денег (ударение в слове «временная» здесь ставится на последний слог) – это экономическая концепция учитывающая изменение стоимости денег с течением времени.

Если говорить простыми словами, то суть данной концепции можно выразить одним предложением: одна и та же сумма денег сегодня стоит дороже, чем завтра и в последующие дни (причем, чем больше промежуток времени, тем больше эта самая разница в стоимости).

Объясняется это также довольно просто, как с экономической, так и с чисто психологической точки зрения. С точки зрения человеческой психологии всегда приятнее получить деньги сегодня, нежели завтра, в следующем месяце или через год. А поэтому одна и та же сумма полученная, что называется, сей момент, всегда оценивается дороже.

Ну а с точки зрения экономики, временная стоимость денег объясняется (и, собственно, оценивается) теми процентами, которые деньги могут принести за конкретный рассматриваемый промежуток времени.

Взять, к примеру, простой вклад в банк. Если вы положили на свой банковский счёт 100000 рублей, а через год сняли с него уже 108000 рублей, то временная стоимость указанной суммы денег за этот период составила 8000 рублей (более корректно будет указать её в процентах – 8% годовых).

В общем и целом из рассматриваемой концепции вытекают два следующих важных принципа:

1. В рамках проведения любых финансовых операций (с платежами, разнесёнными по срокам) следует обязательно учитывать фактор времени при взаиморасчётах;
2. В плане анализа долгосрочных инвестиций (или финансовых операций) некорректно суммировать денежные величины, относящиеся к разным моментам времени (без учёта стоимости денег за рассматриваемые периоды).

Как рассчитать временную стоимость денег

Теперь давайте поговорим о том, как, собственно говоря, эту самую пресловутую стоимость рассчитать. Как уже понятно из вышесказанного, временная стоимость денег в численном выражении является не чем иным, как той прибылью, которую можно бы было извлечь из них (например, посредством инвестирования) за рассматриваемый период времени.

То есть в самом простом случае, например при инвестировании денег в облигации с годовой ставкой доходности в 8%, потерянная прибыль за год будет составлять эти самые 8%. Другими словами, сумма в 100000 рублей, через один год будет оцениваться уже в (100000 + 100000х0,08) = 108000 рублей. И наоборот, будущая сумма (через один год) в 100000 рублей, в настоящее время будет оценена в 100000/1,08 = 92592,59 рублей.

При проведении финансовых операций, все разнесённые во времени платежи приводят к единому моменту времени (дисконтируют). Таким образом и учитывается временная стоимость денег.

Принято различать два основных вида стоимости:

1. Нынешняя стоимость денег (Present value, PV);
2. Будущая стоимость денег (Future value, FV).

Нынешнюю стоимость денег PV ещё называют дисконтированной стоимостью. Для приведённого выше примера (100000 рублей и восьмипроцентных облигаций), нынешняя стоимость денег равна 100000 рублей, а будущая, соответственно, 108000 рублей.

В общем случае, при проведении финансовых расчётов все денежные суммы приводятся либо к PV, либо к FV (за заданный промежуток времени) и только после этого их суммируют (или проводят другие вычисления с ними).

Расчёты величин PV и FV могут проводиться как на основе простого, так и на основе сложного процента.

Напомним, что сложным процентом называется начисление прибыли с учётом реинвестирования. То есть, например, прибыль за пять лет при годовой ставке доходности в 5%, будет считаться с учётом того, что каждый год к инвестируемой сумме добавляются 5% прибыли.

В случае расчёта на основе простого процента, формулы нынешней и будущей стоимости денег будут иметь вид:

где R – процентная ставка (годовых);

T – срок в годах.

При расчёте на основе сложного процента, формулы примут вид:

А, например, для случая аннуитетных платежей со ставкой роста g и ставкой дисконтирования i, нынешнюю стоимость денег (PV) можно рассчитать по формуле:

Что оказывает влияние на временную стоимость денег

Если, что называется, копнуть чуть глубже, то можно сказать, что временная стоимость денег может зависеть как от внутренних, так и от внешних факторов. К внутренним факторам следует отнести такие, которые зависят главным образом от того, каким образом происходит распоряжение деньгами с течением времени. А именно:

1. Уровень доходности (проценты от инвестиций денежных средств);
2. Уровень риска сопряжённый с вышеупомянутыми инвестициями. Риск может заключаться как в неполучении дохода от инвестиций, так и в прямом убытке от них (вплоть до полного невозврата инвестированных средств).

К внешним же факторам относят те, которые не зависят от того каким образом управляются деньги, в какие финансовые инструменты они инвестируются и пр. Самым главным из них является инфляция. Чем выше уровень инфляции, тем больше обесцениваются деньги со временем и, следовательно, тем меньше становится их будущая стоимость (FV).

Для учёта всех этих факторов существуют сложные формулы, позволяющие максимально точно (насколько это вообще возможно) рассчитать временную стоимость денег. Точность таких расчётов во многом ограничена тем, что такие величины как уровень доходности, риск или инфляция берутся исходя из прогнозируемых значений (а любой прогноз имеет свою степень погрешности).

Мы же не стали вникать в такие премудрости и привели простые формулы для расчёта текущей (PV) и будущей (FV) стоимости денег на основе предполагаемого уровня доходности по ним (см. предыдущий раздел). Полагаю, что этого вполне достаточно для того, чтобы понять всю суть излагаемой здесь теории.

Ну а если сказать ещё проще, то с точки зрения простого трейдера или инвестора, рассматриваемая концепция временной стоимости денег может быть сведена к аксиоме: Деньги должны делать деньги.

Чистая приведённая стоимость (ЧПС , чистая текущая стоимость , чистый дисконтированный доход , ЧДД , англ. Net present value , принятое в международной практике для анализа инвестиционных проектов сокращение - NPV ) - это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню.

Метод чистой приведенной стоимости получил широкое применение при бюджетировании капитальных вложений и принятии инвестиционных решений. Также NPV считается лучшим критерием отбора для принятия или отклонения решения о реализации инвестиционного проекта, поскольку основывается на концепции стоимости денег во времени. Другими словами, чистая приведенная стоимость отражает ожидаемое изменение благосостояния инвестора в результате реализации проекта.

Формула NPV

Чистая приведенная стоимость проекта является суммой настоящей стоимости всех денежных потоков (как входящих, так и исходящих). Формула расчета выглядит следующим образом:

• CF t – ожидаемый чистый денежный поток (разница между входящим и исходящим денежным потоком) за период t ,
• r – ставка дисконтирования,
• N – срок реализации проекта.

Ставка дисконтирования

Важно понимать, что при выборе ставки дисконтирования должна быть учтена не только концепция стоимости денег во времени, но и риск неопределенности ожидаемых денежных потоков! По этой причине в качестве ставки дисконтирования рекомендуется использовать средневзвешенную стоимость капитала (англ. Weighted Average Cost of Capital, WACC ), привлеченного для реализации проекта. Другими словами, WACC является требуемой нормой доходности на капитал, инвестированный в проект. Следовательно, чем выше риск неопределенности денежных потоков, тем выше ставка дисконтирования, и наоборот.

Критерий отбора проектов

Правило принятия решения об отборе проектов при помощи NPV метода довольно прямолинейно. Нулевое пороговое значение говорит о том, что денежные потоки проекта позволяют покрыть стоимость привлеченного капитала. Таким образом, критерии отбора можно сформулировать следующим образом:

1. Отдельно взятый независимый проект должен быть принят при положительном значении чистой приведенной стоимости или отклонен при отрицательном. Нулевое значение является точкой безразличия для инвестора.
2. Если инвестор рассматривает несколько независимых проектов, принять следует те из них, у которых наблюдается положительный NPV.
3. Если рассматривается ряд взаимоисключающих проектов, выбрать следует тот из них, у которого будет максимальная чистая приведенная стоимость.

В данной статье мы рассмотрим, что такое чистая текущая стоимость (NPV), какой экономический смысл она имеет, как и по какой формуле рассчитать чистую текущую стоимость, рассмотрим некоторые примеры расчёта, в том числе при помощи формул MS Exel.

Что такое чистая текущая стоимость (NPV)?

При вложении денег в любой инвестиционный проект ключевым моментом для инвестора является оценка экономической целесообразности такого инвестирования. Ведь инвестор стремится не только окупить свои вложения, но и ещё что-то заработать сверх суммы первоначальной инвестиции. Кроме того, задачей инвестора является поиск альтернативных вариантов инвестирования, которые бы при сопоставимых уровнях риска и прочих условиях инвестирования принесли бы более высокую прибыль. Одним из методов подобного анализа является расчёт чистой текущей стоимости инвестиционного проекта.

Чистая текущая стоимость (NPV, Net Present Value) – это показатель экономической эффективности инвестиционного проекта, который рассчитывается путём дисконтирования (приведения к текущей стоимости, т.е. на момент инвестирования) ожидаемых денежных потоков (как доходов, так и расходов).

Чистая текущая стоимость отражает прибыль инвестора (добавочную стоимость инвестиций), которую инвестор ожидает получить от реализации проекта, после того, как денежные притоки окупят его первоначальные инвестиционные затраты и периодические денежные оттоки, связанные с осуществлением такого проекта.

В отечественной практике термин «чистая текущая стоимость» имеет ряд тождественных обозначений: чистая приведённая стоимость (ЧПС), чистый приведённый эффект (ЧПЭ), чистый дисконтированный доход (ЧДД), Net Present Value (NPV).

Формула расчёта NPV

Для расчёта NPV необходимо:

1. Составить прогнозный график по инвестиционному проекту в разрезе периодов. Денежные потоки должны включать как доходы (притоки средств), так и расходы (осуществляемые инвестиции и прочие затраты по реализации проекта).
2. Определить размер . По сути, ставка дисконтирования отражает предельную норму стоимости капитала инвестора. Например, если для инвестирования будут использованы заёмные средства банка, то ставкой дисконтирования будет являться по кредиту. Если же будут использованы собственные средства инвестора, то за ставку дисконтирования может быть взята ставка процента по банковскому депозиту, ставка доходности по государственным облигациям и т.п.

Расчёт NPV осуществляется по следующей формуле:

где
NPV (Net Present Value) — чистая текущая стоимость инвестиционного проекта;
CF (Cash Flow) — денежный поток;
r — ставка дисконтирования;
n — общее количество периодов (интервалов, шагов) i = 0, 1, 2, …, n за весь срок инвестирования.

В данной формуле CF 0 соответствует объёму первоначальных инвестиций IC (Invested Capital), т.е. CF 0 = IC . При этом денежный поток CF 0 имеет отрицательное значение.

Поэтому, вышеуказанную формулу можно модифицировать:

Если инвестиции в проект осуществляются не одномоментно, а на протяжении ряда периодов, то инвестиционные вложения также должны быть продисконтированны. В таком случае формула NPV проекта примет следующий вид:

Практическое применение NPV (чистой текущей стоимости)

Расчёт NPV позволяет оценить целесообразность инвестирования денежных средств. Возможны три варианта значения NPV:

1. NPV > 0 . Если чистая текущая стоимость имеет положительное значение, то это свидетельствует о полной окупаемости инвестиций, а значение NPV показывает итоговый размер прибыли инвестора. Инвестиции являются целесообразными в следствие их экономической эффективности.
2. NPV = 0 . Если чистая текущая стоимость имеет нулевое значение, то это свидетельствует об окупаемости инвестиций, но инвестор при этом не получает прибыль. Например, если были использованы заёмные средства, то денежные потоки от инвестиционных вложений позволят в полном объеме рассчитаться с кредитором, в том числе выплатить причитающиеся ему проценты, но финансовое положение инвестора при этом не изменится. Поэтому следует поискать альтернативные варианты вложения денежных средств, которые бы имели положительный экономический эффект.
3. NPV < 0 . Если чистая текущая стоимость имеет отрицательное значение, то инвестиция не окупается, а инвестор в таком случае получает убыток. От вложения средств в такой проект следует отказаться.

Таким образом, к инвестированию принимаются все проекты, которые имеют положительное значение NPV. Если же инвестору необходимо сделать выбор в пользу только одного из рассматриваемых проектов, то при прочих равных условиях предпочтение следует отдать тому проекту, который имеет наибольшее значение NPV.

Расчёт NPV при помощи MS Exel

В MS Exel существует функция ЧПС, позволяющая осуществить расчёт чистой приведённой стоимости.

Функция ЧПС возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также стоимости будущих выплат (отрицательные значения) и поступлений (положительные значения).

Синтаксис функции ЧПС:

ЧПС(ставка;значение1;значение2; ...)

где
Ставка — ставка дисконтирования за один период.
Значение1, значение2,… - от 1 до 29 аргументов, представляющих расходы и доходы .

Значение1, значение2, … должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.

ЧПС использует порядок аргументов значение1, значение2, … для определения порядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в правильном порядке.

Рассмотрим пример расчёта NPV на базе 4-х альтернативных проектов.

В результате проведённых расчётов проект А следует отклонить, проект Б находится в точке безразличия для инвестора, а вот проекты В и Г следует использовать для вложения средств. При этом, если необходимо выбрать только один проект, то предпочтение следует отдать проекту В , невзирая на то, что сумму недисконтированных денежных потоков за 10 лет он генерирует меньше, чем проект Г .

Преимущества и недостатки NPV

К положительным моментам методики NPV можно отнести:

• чёткие и простые правила для принятия решений относительно инвестиционной привлекательности проекта;
• применение ставки дисконтирования для корректировки суммы денежных потоков во времени;
• возможность учета премии за риск в составе ставки дисконтирования (для более рискованных проектов можно применить повышенную ставку дисконтирования).

К недостаткам NPV можно отнести следующие:

• трудность оценки для сложных инвестиционных проектов, которые включают в себя множество рисков особенно в долгосрочной перспективе (требуется корректировка ставки дисконтирования);
• сложность прогнозирования будущих денежных потоков, от точности которых зависит расчетная величина NPV;
• формула NPV не учитывает реинвестирование денежных потоков (доходов);
• NPV отражает только абсолютную величину прибыли. Для более корректного анализа необходимо также дополнительно производить расчёт и относительных показателей, например таких как , .

Определения настоящей (текущей) стоимости денег

В финансовых расчетах существует необходимость сравнивать между собой различные суммы денег в разные моменты времени. Именно поэтому достаточно часто возникает необходимость определения настоящей (текущей) стоимости (Present Value - PV) денег, которая выступает основой для сравнения прибыльности различных проектов и инвестиций за определенный период.

Нынешняя стоимость - это денежная стоимость будущих поступлений или доходов с поправкой на ставки дисконта (капитализации).

С формальной точки зрения, ставка дисконтирования - это процентная ставка, используемая для приведения будущих поступлений (денежных потоков и прибыли) к настоящей стоимости. Ставка дисконтирования выражается в процентах или долях единицы. Верхний уровень ставки дисконтирования теоретически может быть больше 100 % (больше 1), а нижний уровень определяется экономическими факторами. С экономической точки зрения ставка дисконтирования - мера затрат на привлечения капитала для инвестирования в конкретный инвестиционный проект.

Иначе говоря, ставка дисконтирования-это ожидаемая инвесторами ставка доходности на вложенный капитал при наличии альтернативных возможностей его вложения в объекты инвестиций с аналогичным уровнем риска. В связи с этим нижним уровнем ставки дисконтирования является так называемая "безрисковая" ставка. По сути, это такая ставка процента, под которую инвесторы могли бы дать деньги в долг, если бы не было опасности вернуть их обратно, или под которую они могли бы взять деньги в долг, если бы их залоговое обеспечение было бы настолько надежным, что кредиторы считали бы шансы на неуплату мизерными.

В странах с развитой рыночной экономикой как "безрисковую" ставку используют процент по ценным бумагам, гарантированным правительством США, или текущую ставку доходности по казначейским векселям и облигациям. В отдельных крупных проектах, которые предусматривают финансирование как за счет отечественного, так и иностранного капитала, уровень "безрисковой" ставки принимают по ставке LIBOR (процентная ставка, по которой на европейском валютном рынке банки предлагают друг другу депозиты). Для условий Украины вопрос установления уровня "безрисковой" ставки не может быть определен однозначно. Одной из основных причин этого является отсутствие сложившегося рынка капитала внутри страны.

Для подсчета текущей стоимости следует определить ставку дисконта, учитывающей рискованность определенного проекта или инвестиций. Существует простое правило:

риск означает высокую ставку дисконта (капитализации), малый риск означает низкую дисконтную ставку.

в Целом для оценки дисконтных ставок используют такие принципы:

из двух будущих поступлений высшее учетную ставку будет иметь то, что поступит позже;

чем ниже определенный уровень риска, тем ниже должна быть ставка дисконта; если общие процентные ставки на рынке растут, растут и дисконтные ставки; риск может уменьшиться, если есть перспектива делового подъема, снижение др..

Расчет настоящей стоимости денег осуществляется с помощью процесса дисконтирования, который является противоположным компаундуванню.

Дисконтирование - это нахождение начальной или текущей суммы долга (PV) по известной конечной сумме (FV)% которую нужно отдать через некоторое время (п). то Есть дисконтирование - это процесс возведения экономических показателей разных лет к сопоставимого во времени виду.

Говорят: сумма FV - дисконтируется, а разность FV - PV называется дисконтом и обозначается D. Дисконт - это процентные деньги (проценты), начисленные и собранные заранее.

в условиях рынка задача дисконтирования возникает очень часто при выработке условий контрактов между двумя предприятиями, различными объектами хозяйствования, при определении текущей рыночной стоимости векселей, акций, облигаций и других ценных бумаг.

Практическое применение дисконтирования для определения приведенной настоящей стоимости денежных потоков требует соответствующего финансово-математической формализации модели дисконтирования - определение абсолютной величины дисконта. В зависимости от потребностей анализа денежных потоков и изменения их стоимости во времени могут использоваться такие модели дисконтирования: простое дисконтирования аннуитетов (отсроченной или авансовой ренты) - подробно будет рассмотрено в параграфе 4.4.

простым дисконтированием (single discounting) понимают финансово-математическая модель расчета приведенной стоимости будущего денежного потока, получение которого, как ожидается, состоится однократно через четко определенный период. Результатом простого дисконтирования является приведенная настоящая стоимость (present value, или PV) отдельного будущего денежного потока.

Процессы компаундирования и дисконтирования тесно взаимосвязаны друг с другом. Определение текущей стоимости (дисконтирования) является прямой противоположностью компаундуванню, то есть эти величины характеризуются обратной зависимостью:

Таким образом, если нам известен показатель будущей стоимости денег (РУ), то с помощью дисконтирования мы можем рассчитать их приведенную стоимость (РУ).

Дисконтирование осуществляется с помощью коэффициента дисконтирования (дисконтуючого множителя, а1).

Определим учетную ставку d, как следующее отношение:

Настоящая стоимость денег может определяться исходя из простой или сложной схемы начисления процентов.

Пользуясь соотношением (4.15) и учитывая зависимость между функциями компаундингу и дисконтирования, приведем формулу для определения текущей стоимости денег в случае использования дисконтной ставки для схемы простых процентов:

где РУ- приведенная текущая стоимость будущего денежного потока; РУ - абсолютная величина будущего денежного потока; п - количество интервалов в плановом периоде; г - ставка дисконтирования (выраженная десятичной дробью); Као - коэффициент дисконтирования при применении простых процентов (выраженный десятичной дробью).

Пример . Какую сумму надо положить на депозитный счет инвестору, чтобы в конце четвертого года получить 25000 игры., если проценты установлены на уровне 16% и начисляются они по простой схеме?

При учете инфляции, как и в случае определения будущей стоимости, результат корректируется путем учета ее прогнозного уровня (Ипр):

где / - прогнозный уровень инфляции;

Дисконтирование с использованием сложных процентов является достаточно распространенным способом определения текущей стоимости денег, которая используется не только в финансовом менеджменте, но и в инвестиционном проектировании и при определении стоимости бизнеса.

Задача определения настоящей стоимости по схеме сложных процентов решают с помощью формулы 4.19:

где---- это коэффициент дисконтирования. Экономический коэффициент дисконтирования

состоит в том, что его величина соответствует текущей стоимости одной денежной единицы, которая будет получена в конце периода п при сложном процента г. Его величина зависит от длительности всего периода и необходимой ставки дисконта.

Пример . Допустим, что кое-кто хотел бы иметь через 4 года 1000 игры., недостающие до суммы уплаты за обучение ребенка в престижном университете. Если средняя ставка по депозитам составляет 15%, какую сумму ему необходимо отнести в банк?

Можно определить настоящую стоимость будущего денежного потока с использованием финансовой таблицы (Приложение Б), которая содержит абсолютное значение ставки дисконтирования, исходя из уровня процентной ставки и количества интервалов в плановом периоде. Таблица определения настоящей стоимости экономит много усилий для подсчета различных ее факторов. Эта таблица, например, показывает, что стоимость уменьшается, когда возрастает промежуток времени, а также когда повышается ставка дисконта.

Приложении Б приведены только те значения факторов, которые, если их перемножить на будущую стоимость, дают значение приведенной стоимости. Соответственно с учетом данных финансовой таблицы с Приложении Б нынешнюю стоимость рассчитывают по формуле 4. 20:

где PVIF- фактор (множитель) текущей стоимости, стандартные значения которого приведены в таблице значений фактора текущей стоимости (Приложение Б).

Пример . Допустим, вы хотите определить нынешнюю стоимость $ 1000 через годы; вы надеетесь на ежегодный уровень риска, связанный с реализацией проектов под 10%.

Как видно из Приложения А, значения факторов растет от времени и роста сложного процента. Поэтому, если эти факторы подставить в знаменатель последнего уравнения, нынешняя стоимость $ 1000 через 3 года будет:

$ 1000/(1+0,10)* = $ 751

Как появилась эта стоимость? Путем простого перемножения (1,10 х 1,10 х 1,10= 1,33) и использование этого фактора для дисконтирования: $ 1000/1,33 = $751

В последнем примере, где стояла задача определить текущую стоимость $1000 через 3 года, достаточно было посмотреть на количество лет и соответствующий процентный фактор нынешней стоимости (PVIF) Present Value interest Factor согласно поданной дисконтной ставке. Как показано в Приложении Б, этот фактор составляет 0,751. Чтобы получить теперешнюю стоимость $1000 через 3 года, имея дисконт 10%, перемножте значения фактора на сумму текущей стоимости($1000*(0751 = $751). Тот же результат вы получили путем длинных подсчетов.

Если начисление процентов планируется более одного раза за год, то расчет проводят по формуле 4. 21:

где т - количество начислений за год, ед.

процента, начисляемую непрерывно настоящая стоимость средств определяется по формуле 4. 22:

Настоящая стоимость является суммой денег, которая, если ее инвестировать в текущем году под данный процент г вырастет через // лет в будущем до необходимого или желаемого уровня. Теперешняя стоимость - это единственный правильный путь для конвертации потоков будущих платежей в сегодняшние деньги.

Очевидно, если вы имеете два разных проекта с одинаковым периодом реализации и расходами, но разными факторами риска, то можно определить их настоящую стоимость и сравнить, какой из них целесообразнее выбрать. Оценка целесообразности капиталовложений в те или иные проекты или инвестиции в основу берет понятие приведенной стоимости. Все сводится к тому, чтобы дисконтировать будущий доход в зависимости от уровня риска и неопределенности будущего. Метод определения текущей стоимости позволяет это сделать.

Пример . Допустим, фирма надеется получить такие суммы денег за следующие четыре года: 1-й год - 1000 тыс. игры.; 2-й год -1200 тыс. грн.; 3-й год -1500 тыс. грн.; 4-й год - 900 тыс. грн.

Нынешняя стоимость всего денежного потока является простой суммой стоимости денежных потоков за каждый год. Если дисконтная ставка равна 10%, текущая стоимость денежных потоков за 4 года равна 3642,43 тыс. грн.:

Настоящая стоимость денежного потока за 4 года составляет 3642,43 тыс. грн.

Таблица настоящей стоимости (Приложение Б) очевидно экономит финансистам много времени. Обратите внимание на то, что за понижение ставки дисконта растет значение приведенной стоимости, когда ставки растут - стоимость падает. Следовательно, должно быть понятно, что понятие настоящей стоимости является важным фактором для выбора решения о вложении денег и инвестиций.

Из этой статьи вы узнаете:

• Как определить вероятную прибыльность проекта
• Как выяснить, стоит ли делать инвестиции в проект
• Что такое NPV инвестиционного проекта
• Какова формула расчета NPV для нового проекта
• Как точно вычислить ЧДД для определенного проекта

Чистая приведенная стоимость (NPV) входит в число самых важных показателей, позволяющих принимать решение о целесообразности инвестиций в проект. Обычно этот показатель используется в области корпоративных финансов, но при необходимости может быть применен для постоянного мониторинга общей финансовой ситуации. Вне зависимости от сферы использования, очень важно понимать, как рассчитать NPV правильно для инвестиционного проекта и какие трудности могут встретиться в процессе этой работы.

Что такое NPV простыми словами

NPV называют чистую стоимость денежных потоков, приведенную к моменту расчета проекта. Благодаря формуле расчета NPV удается оценить собственную экономическую эффективность проекта и сравнить между собой несколько объектов инвестирования.

Английская аббревиатура NPV (Net Present Value) имеет в русском языке несколько аналогов:

• Чистая приведенная стоимость (ЧПС). Этот вариант является наиболее распространенным, даже в «Microsoft Excel» формула называется именно таким образом.
• Чистый дисконтированный доход (ЧДД). Название связано с тем, что денежные потоки дисконтируются и лишь после этого суммируются.
• Чистая текущая стоимость (ЧТС). Все доходы и убытки от деятельности за счет дисконтирования приводятся к текущей стоимости денег. Поясним: с точки зрения экономики, если мы заработаем 1000 руб., то получим потом на самом деле меньше, чем если бы мы получили ту же сумму прямо сейчас.

Дисконтирование - это определение стоимости денежного потока путём приведения стоимости всех выплат к определённому моменту времени. Дисконтирование является базой для расчётов стоимости денег с учётом фактора времени.

NPV представляет собой уровень прибыли, который ожидает участников инвестиционного проекта. Математически этот показатель определяют за счет дисконтирования значений чистого денежного потока, при этом неважно, о каком потоке идет речь: отрицательном либо положительном.

Если максимально упростить определение, то NPV – это доход, который получит владелец проекта за период планирования, оплатив все текущие затраты и рассчитавшись с налоговыми органами, персоналом, кредитором (инвестором), в том числе выплатив проценты (или с учетом дисконтирования).

Допустим, за 10 лет планирования предприятие получило выручку в 5,57 млрд руб., тогда как общая сумма налогов и всех затрат равна 2,21 млрд руб. Значит, сальдо от основной деятельности окажется 3,36 млрд руб.

Но это пока не искомый результат – из данной суммы нужно вернуть первоначальные инвестиции, допустим, 1,20 млрд руб. Чтобы упростить подсчет, будем считать, что проект финансируется за счет средств инвестора по нулевой ставке дисконтирования. Тогда, если рассчитать показатель NPV, он составит 2,16 млрд руб. за 10 лет планирования.

Если увеличить срок планирования, то увеличится и размер ЧДД. Смысл этого показателя в том, что он позволяет рассчитать еще на этапе разработки бизнес-плана, какой реальный доход может получить инициатор проекта.

Повторим, что NPV – один из ключевых показателей оценки эффективности инвестиционных проектов. Поэтому если рассчитать его даже с малейшей неточностью, можно столкнуться с потенциально неэффективным вложением средств.

Зачем нужен показатель NPV

Если у вас на примете есть перспективный бизнес-проект, в который вы готовы вложить деньги, советуем рассчитать его чистую приведенную стоимость.

1. Оцените денежные потоки от проекта, то есть первоначальное вложение (отток) и ожидаемые поступления (притоки) денежных средств.
2. Определите стоимость капитала (cost of capital), так как этот показатель станет для вас ставкой дисконтирования.
3. Продисконтируйте притоки и оттоки от проекта по ставке, которую вам удалось рассчитать на предыдущем шаге.
4. Сложите все дисконтированные потоки – это и будет NPV проекта.

На самом деле, все просто – если NPV равен нулю, значит, денежных потоков от проекта хватит, чтобы:

• возместить инвестированный капитал;
• обеспечить доход на этот капитал.

При положительном NPV проект принесет прибыль, и чем выше его уровень, тем выгоднее окажутся вложения в проект.

Кредиторы, то есть люди, дающие деньги в долг, имеют фиксированный доход, поэтому все средства, превышающие этот показатель, остаются акционерам. Если компания решает одобрить проект с нулевым NPV, акционеры сохранят свою позицию – компания станет больше, но акции не поднимутся в цене. При положительном NPV проекта акционеры станут богаче.

NPV позволяет рассчитать, какой из инвестиционных проектов выгоднее, когда их несколько, но компания не имеет средств на реализацию сразу всех. В этом случае приступают к проектам с наибольшей возможностью заработать или с самым высоким NPV.

• четкие критерии принятия решения об инвестировании – первоначальные инвестиции, выручка на каждом этапе, доходность альтернативных вложений;
• учет изменения стоимости денег с течением времени;
• учет рисков за счет использования различных ставок дисконтирования.

Но не стоит заблуждаться и считать этот показатель абсолютно точным коэффициентом. Нередко сложно корректно рассчитать ставку дисконтирования, особенно когда речь идет о многопрофильных проектах. Также отметим, что при расчете не учитывается вероятность исхода каждого проекта.

Формула расчета NPV

Как рассчитать чистый дисконтированный доход NPV? Казалось бы, все просто: нужно вычесть из всех притоков денежных средств все оттоки по каждому временному отрезку, после чего привести полученные значения к моменту расчета.

• IC – сумма первоначальных инвестиций;
• N – число периодов (месяцев, кварталов, лет), за которые нужно рассчитать оцениваемый проект;
• t – отрезок времени, для которого необходимо рассчитать чистую приведенную стоимость;
• i – расчетная ставка дисконтирования для оцениваемого варианта вложения инвестиций;
• CFt – ожидаемый денежный поток (чистый) за установленный временной период.

Пример того, как рассчитать NPV

Известно, что в бизнес было инвестировано 500 тыс. рублей.

Ожидаемые доходы (CFt) за 5 лет составят:

• 2014 год – 100 тыс. рублей;
• 2015 год – 150 тыс. рублей;
• 2016 год – 200 тыс. рублей;
• 2017 год – 250 тыс. рублей;
• 2018 год – 300 тыс. рублей.

Ставка дисконтирования равна 20 %.

Решение задачи:

где CFt – денежные потоки по годам;

r – ставка дисконтирования;

t – номер года по счету.

Тогда в первый год чистый денежный поток будет равен CFt / (1 + r) × t = 100000 / (1 + 0,2) 1 = 83 333,33 рублей.

Во второй год этот показатель составит CFt / (1 + r) × t = 150000 / (1 + 0,2) 2 = 104 166,67 рублей.

В третий год получится результат CFt / (1 + r) × t = 200000 / (1 + 0,2) 3 = 115 740,74 рублей.

В четвертый год чистый денежный поток окажется равен CFt / (1 + r) × t = 250000 / (1 + 0,2) 4 = 120 563,27 рублей.

В пятый год – CFt / (1 + r) × t = 300000 / (1 + 0,2) 5 = 120 563,27 рублей.

∑CFi / (1 + r) × i = 83333,33 + 104166,67 + 115740,74 + 120563,27 + 120563,27 = 544 367,28 рублей.

Применяем уже упомянутую выше формулу расчета и получаем:

NPV = - 500 000 + 83 333,33 + 104 166,67 + 115 740,74 + 120 563,27 + 120 563,27 = 44 367,28 рублей.

NPV= 44 367,28 рублей.

Напомним: чтобы инвестиции оправдались, итоговый показатель должен быть положительным. В нашем примере он положителен.

Как рассчитать NPV инвестиционного проекта: пошаговая инструкция

• Определите сумму начальных инвестиций.

Часто средства инвестируются, чтобы приносить прибыль в долгосрочной перспективе. Так, строительная компания может приобрести бульдозер и получить возможность заниматься крупными проектами, а значит, больше зарабатывать. У подобных инвестиций всегда есть первоначальный размер.

Допустим, вы владелец ларька и занимаетесь продажей апельсинового сока. Вы собираетесь купить электрическую соковыжималку, чтобы повысить объемы производимого сока. Если соковыжималка стоит $100, то $100 – это начальные инвестиции, со временем с их помощью вы заработаете больше. Если изначально правильно рассчитать NPV, то можно понять, стоит ли покупать соковыжималку.

• Решите, какой период времени нужно анализировать.

Приведем еще один пример: обувная фабрика покупает дополнительное оборудование, поскольку стремится расширить производство и заработать больше за конкретный промежуток времени. То есть до тех пор, пока данное оборудование не выйдет из строя. Поэтому чтобы рассчитать ЧДД, нужно представлять себе период, за который вложенные средства смогут окупиться. Этот срок может измеряться в любых единицах времени, но обычно за один временной период принимают один год.

Вернемся к примеру с соковыжималкой – на нее дается гарантия на 3 года. Значит, перед нами три временных периода, так как высока вероятность, что спустя три года соковыжималка выйдет из строя и перестанет приносить дополнительные средства.

• Определите поток платежей в течение одного временного периода.

То есть вам нужно рассчитать поступления средств, которые появляются за счет ваших инвестиций. Поток платежей может быть известным или оценочным значением. Во втором случае компании и финансовые фирмы тратят много времени и нанимают соответствующих специалистов и аналитиков для его получения.

Предположим, по вашему мнению, покупка соковыжималки за $100 принесет дополнительные $50 в первый год, $40 во второй год и $30 в третий год. Это произойдет благодаря сокращению времени, затрачиваемого на производство сока, и затрат на зарплату сотрудников. Тогда поток платежей может быть представлен таким образом: $50 за 1 год, $40 за 2 год, $30 за 3 год.

• Определите ставку дисконтирования.

Существует правило, согласно которому любая сумма в настоящий момент имеет большую ценность, чем в будущем. Сегодня вы можете положить ее в банк, а через какое-то время получить ее с процентами. Иными словами, $10 сегодня стоят больше, чем $10 в будущем, ведь вы можете инвестировать $10 сегодня и получить взамен больше $11. Так как нам нужно рассчитать NPV, необходимо знать процентную ставку на инвестиционный счет или инвестиционную возможность с аналогичным уровнем риска. Она называется ставкой дисконтирования – для вычисления нужного нам показателя ее надо представить в виде десятичной дроби.

Нередко компании используют средневзвешенную стоимость капитала, чтобы рассчитать ставку дисконтирования. В простых случаях допускается использование нормы доходности по сберегательному счету, инвестиционному счету, пр. Иными словами, счету, на который можно положить деньги под проценты.

В нашем примере, если вы откажитесь от соковыжималки, вы сможете вложить те же средства в фондовый рынок, где заработаете 4 % годовых от вложенной суммы. Тогда 0,04 или 4 % – это ставка дисконтирования.

• Дисконтируйте денежный поток.

Для этого используйте формулу P / (1 + i) × t, где P – денежный поток, i – процентная ставка и t – время. Пока можно не задумываться о начальных инвестициях, но они будут нужны нам при следующих расчетах.

Напомним, что в нашем случае три временных периода, поэтому рассчитать показатель по формуле придется трижды. Так будет выглядеть вычисление ежегодных дисконтированных денежных потоков:

1. Год 1: 50 / (1 + 0,04) × 1 = 50 / (1,04) = $48,08;
2. Год 2: 40 / (1 +0,04) × 2 = 40 / 1,082 = $36,98;
3. Год 3: 30 / (1 +0,04) × 3 = 30 / 1,125 = $26,67.

• Сложите значения дисконтированных денежных потоков и вычтите из результата начальные инвестиции.

У вас получиться рассчитать сумму средств, которую принесут вложенные инвестиции, по сравнению с доходом от альтернативных инвестиций под ставку дисконтирования. Повторим, что если перед вами положительное число, то вы заработаете больше денег на инвестициях, чем на альтернативных инвестициях. И наоборот, если число отрицательное. Но не стоит забывать, что точность результата зависит от того, насколько верно удалось рассчитать будущие потоки денежных средств и ставку дисконтирования.

48,08 + 36,98 + 26,67 - 100 = $11,73.

• Если NPV – положительное число, проект принесет прибыль.

Вы получили отрицательный результат? Тогда лучше инвестировать средство в другой проект или пересмотреть имеющийся. Если отойти от примеров, то данный показатель позволяет понять, стоит ли в принципе вкладывать деньги в определенный проект.

В нашем примере с соковыжималкой ЧДД = $11,73. Поскольку мы получили положительное число, вы, вероятно, решитесь на покупку.

Подчеркнем, полученная цифра не значит, что за счет соковыжималки вы выиграете всего $11,73. Этот показатель говорит о том, что вы получите сумму на $11,73 больше, чем та, которую вы бы получили, вложив деньги в фондовый рынок под 4 % годовых.

Как рассчитать NPV в «Microsoft Excel»

В «Microsoft Excel» есть формула, которая рассчитывает чистую приведенную стоимость. Для этого вам нужно знать ставку дисконтирования (указывается без знака «проценты») и выделить диапазон чистого денежного потока. Вид формулы такой: = ЧПС (процент; диапазон чистого денежного потока) - инвестиции.

На создание подобной таблицы уходит не больше 3-4 минут, то есть благодаря «Microsoft Excel» вы сможете рассчитать необходимое значение гораздо быстрее.

Возможные сложности при расчете NPV

При работе с NPV мало знать, что это такое и как рассчитать, нужно также представлять пару важных тонкостей.

Начнем с того, что данный показатель трудно объяснить тем, кто не занимается финансами.

Фразу «дисконтированная стоимость будущих денежных потоков» нелегко заменить при общении на «нефинансовом» языке. Однако этот показатель стоит того, чтобы потратить силы на его объяснение. Любая инвестиция, которая проходит тест ЧДД, повышает акционерную стоимость. И наоборот, инвестиции, которые этот тест не прошли, точно нанесут урон компании и акционерам.

Также менеджеры не должны забывать: чтобы рассчитать NPV, нужно основываться на нескольких предположениях и оценках. Иными словами, расчет может быть субъективен и содержать ошибки. Можно снизить риски, дважды проверив свои оценки и сделав анализ чувствительности после первоначального расчета.

Ошибочные оценки сильно скажутся на конечных результатах расчета – все они могут возникнуть в трех случаях:

• Первоначальные инвестиции. Вы знаете, в какую сумму обойдутся проект или расходы? При покупке оборудования по фиксированной цене такой риск отсутствует. Но если вы обновляете свою ИТ-систему, и ваши затраты на персонал зависят от сроков и этапов проекта, а также вы собираетесь делать предполагаемые закупки, суммы оказываются достаточно условными.
• Риски, связанные со ставкой дисконтирования. Вы используете сегодняшнюю ставку, чтобы рассчитать будущие доходы, но может быть так, что на третьем году проекта процентные ставки будут расти, а стоимость ваших средств увеличится. То есть ваши доходы за этот год окажутся менее ценными, чем вы планировали.
• Прогнозируемые результаты проекта. Именно здесь финансовые аналитики часто ошибаются в оценке, когда решают рассчитать NPV и PI. Вам важно быть уверенными в прогнозируемых результатах вашего проекта. Обычно прогнозы оптимистичны, ведь люди хотят делать проект или закупать оборудование.