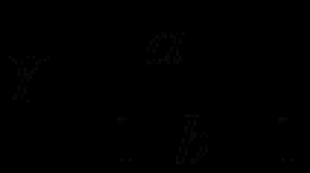Ипотека

Как рассчитывается внутренняя норма доходности. Расчет NPV в Excel (пример)

Каждый человек, который серьезно занимался финансовой деятельностью или профессиональным инвестированием, сталкивался с таким показателем, как чистый дисконтированный доход или NPV . Этот показатель отражает инвестиционную эффективность изучаемого проекта. В программе Excel имеются инструменты, которые помогают рассчитать это значение. Давайте выясним, как их можно использовать на практике.

Показатель чистого дисконтированного дохода (ЧДД) по-английски называется Net present value, поэтому общепринято сокращенно его называть NPV . Существует ещё альтернативное его наименование – Чистая приведенная стоимость.

NPV определяет сумму приведенных к нынешнему дню дисконтированных значений платежей, которые являются разностью между притоками и оттоками. Если говорить простым языком, то данный показатель определяет, какую сумму прибыли планирует получить инвестор за вычетом всех оттоков после того, как окупится первоначальный вклад.

В программе Excel имеется функция, которая специально предназначена для вычисления NPV . Она относится к финансовой категории операторов и называется ЧПС . Синтаксис у этой функции следующий:

ЧПС(ставка;значение1;значение2;…)

Аргумент «Ставка» представляет собой установленную величину ставки дисконтирования на один период.

Аргумент «Значение» указывает величину выплат или поступлений. В первом случае он имеет отрицательный знак, а во втором – положительный. Данного вида аргументов в функции может быть от 1 до 254 . Они могут выступать, как в виде чисел, так и представлять собой ссылки на ячейки, в которых эти числа содержатся, впрочем, как и аргумент «Ставка» .

Проблема состоит в том, что функция хотя и называется ЧПС , но расчет NPV она проводит не совсем корректно. Связано это с тем, что она не учитывает первоначальную инвестицию, которая по правилам относится не к текущему, а к нулевому периоду. Поэтому в Экселе формулу вычисления NPV правильнее было бы записать так:

Первоначальная_инвестиция+ ЧПС(ставка;значение1;значение2;…)

Естественно, первоначальная инвестиция, как и любой вид вложения, будет со знаком «-» .

Пример вычисления NPV

Давайте рассмотрим применение данной функции для определения величины NPV на конкретном примере.

Выделяем ячейку, в которой будет выведен результат расчета NPV . Кликаем по значку «Вставить функцию» , размещенному около строки формул.

Запускается окошко Мастера функций . Переходим в категорию «Финансовые» или «Полный алфавитный перечень» . Выбираем в нем запись «ЧПС» и жмем на кнопку «OK» .

После этого будет открыто окно аргументов данного оператора. Оно имеет число полей равное количеству аргументов функции. Обязательными для заполнения является поле «Ставка» и хотя бы одно из полей «Значение» .
В поле «Ставка» нужно указать текущую ставку дисконтирования. Её величину можно вбить вручную, но в нашем случае её значение размещается в ячейке на листе, поэтому указываем адрес этой ячейки.

В поле «Значение1» нужно указать координаты диапазона, содержащего фактические и предполагаемые в будущем денежные потоки, исключая первоначальный платеж. Это тоже можно сделать вручную, но гораздо проще установить курсор в соответствующее поле и с зажатой левой кнопкой мыши выделить соответствующий диапазон на листе.

Так как в нашем случае денежные потоки размещены на листе цельным массивом, то вносить данные в остальные поля не нужно. Просто жмем на кнопку «OK» .

Расчет функции отобразился в ячейке, которую мы выделили в первом пункте инструкции. Но, как мы помним, у нас неучтенной осталась первоначальная инвестиция. Для того, чтобы завершить расчет NPV , выделяем ячейку, содержащую функцию ЧПС . В строке формул появляется её значение.

После символа «=» дописываем сумму первоначального платежа со знаком «-» , а после неё ставим знак «+» , который должен находиться перед оператором ЧПС .

Можно также вместо числа указать адрес ячейки на листе, в которой содержится первоначальный взнос.

Для того чтобы совершить расчет и вывести результат в ячейку, жмем на кнопку Enter .

Результат выведен и в нашем случае чистый дисконтированный доход равен 41160,77 рублей. Именно эту сумму инвестор после вычета всех вложений, а также с учетом дисконтной ставки, может рассчитывать получить в виде прибыли. Теперь, зная данный показатель, он может решать, стоит ему вкладывать деньги в проект или нет.

Как видим, при наличии всех входящих данных, выполнить расчет NPV при помощи инструментов Эксель довольно просто. Единственное неудобство составляет то, что функция, предназначенная для решения данной задачи, не учитывает первоначальный платеж. Но и эту проблему решить несложно, просто подставив соответствующее значение в итоговый расчет.

NPV (аббревиатура, на английском языке - Net Present Value), по-русски этот показатель имеет несколько вариаций названия, среди них:

чистая приведенная стоимость (сокращенно ЧПС) - наиболее часто встречающееся название и аббревиатура, даже формула в Excel именно так и называется;
чистый дисконтированный доход (сокращенно ЧДС) - название связано с тем, что денежный потоки дисконтируются и только потом суммируются;
чистая текущая стоимость (сокращенно ЧТС) - название связано с тем, что все доходы и убытки от деятельности за счет дисконтирования как бы приводятся к текущей стоимости денег (ведь с точки зрения экономики, если мы заработаем 1 000 руб. и получим потом на самом деле меньше, чем если бы мы получили ту же сумму, но сейчас).

NPV - это показатель прибыли, которую получат участники инвестиционного проекта. Математически этот показатель находится путем дисконтирования значений чистого денежного потока (вне зависимости от того отрицательный он или положительный).

Чистый дисконтированный доход может быть найден за любой период времени проекта начиная с его начала (за 5 лет, за 7 лет, за 10 лет и так далее) в зависимости от потребности расчета.

Для чего нужен

NPV - один из показателей эффективности проекта, наряду с IRR , простым и дисконтированным сроком окупаемости . Он нужен, чтобы:

понимать какой доход принесет проект, окупится ли он в принципе или он убыточен, когда он сможет окупиться и сколько денег принесет в конкретный момент времени;
для сравнения инвестиционных проектов (если имеется ряд проектов, но денег на всех не хватает, то берутся проекты с наибольшей возможностью заработать, т.е. наибольшим NPV).

Формула расчета

Для расчета показателя используется следующая формула:

CF - сумма чистого денежного потока в период времени (месяц, квартал, год и т.д.);
t - период времени, за который берется чистый денежный поток;
N - количество периодов, за который рассчитывается инвестиционный проект;
i - ставка дисконтирования, принятая в расчет в этом проекте.

Пример расчета

Для рассмотрения примера расчета показателя NPV возьмем упрощенный проект по строительству небольшого офисного здания. Согласно проекту инвестиций планируются следующие денежные потоки (тыс. руб.):

Статья	1 год	2 год	3 год	4 год	5 год
Инвестиции в проект	100 000
Операционные доходы		35 000	37 000	38 000	40 000
Операционные расходы		4 000	4 500	5 000	5 500
Чистый денежный поток	- 100 000	31 000	32 500	33 000	34 500

Коэффициент дисконтирования проекта - 10%.

Подставляя в формулу значения чистого денежного потока за каждый период (там где получается отрицательный денежный поток ставим со знаком минус) и корректируя их с учетом ставки дисконтирования получим следующий результат:

NPV = - 100 000 / 1.1 + 31 000 / 1.1 2 + 32 500 / 1.1 3 + 33 000 / 1.1 4 + 34 500 / 1.1 5 = 3 089.70

Чтобы проиллюстрировать как рассчитывается NPV в Excel, рассмотрим предыдущий пример заведя его в таблицы. Расчет можно произвести двумя способами

В Excel имеется формула ЧПС, которая рассчитывает чистую приведенную стоимость, для этого вам необходимо указать ставку дисконтирования (без знака проценты) и выделить диапазон чистого денежного потока. Вид формулы такой: = ЧПС (процент; диапазон чистого денежного потока).
Можно самим составить дополнительную таблицу, где продисконтировать денежный поток и просуммировать его.

Ниже на рисунке мы привели оба расчета (первый показывает формулы, второй результаты вычислений):

Как вы видите, оба метода вычисления приводят к одному и тому же результату, что говорит о том, что в зависимости от того, чем вам удобнее пользоваться вы можете использовать любой из представленных вариантов расчета.

Для расчета внутренней ставки доходности (внутренней нормы доходности, IRR) в Excel используется функция ВСД. Ее особенности, синтаксис, примеры рассмотрим в статье.

Особенности и синтаксис функции ВСД

Один из методов оценки инвестиционных проектов – внутренняя норма доходности. Расчет в автоматическом режиме можно произвести с помощью функции ВСД в Excel. Она находит внутреннюю ставку доходности для ряда потоков денежных средств. Финансовые показатели должны быть представлены числовыми значениями.

Суммы внутри потоков могут колебаться. Но поступления регулярные (каждый месяц, квартал или год). Это обязательное условие для корректного расчета.

Внутренняя ставка доходности (IRR, внутренняя норма доходности) – процентная ставка инвестиционного проекта, при которой приведенная стоимость денежных потоков равняется нулю. При данной ставке инвестор вернет вложенные первоначально средства. Инвестиции состоят из платежей (суммы со знаком «–») и доходов (со знаком «+»), которые происходят в одинаковые по продолжительности временные промежутки.

Аргументы функции ВСД в Excel:

Значения. Диапазон ячеек, в которых содержатся числовые выражения денежных средств. Для данных сумм нужно посчитать внутреннюю норму доходности.
Предположение. Цифра, которая предположительно близка к результату. Аргумент необязательный.

Секреты работы функции ВСД (IRR):

В диапазоне с денежными суммами должно содержаться хотя бы одно положительное и одно отрицательное значение.
Для функции ВСД важен порядок выплат или поступлений. То есть денежные потоки должны вводится в таблицу в соответствии со временем их возникновения.
Текстовые или логические значения, пустые ячейки при расчете игнорируются.
В программе Excel для подсчета внутренней ставки доходности используется метод итераций (подбора). Формула производит циклические вычисления с того значения, которое указано в аргументе «Предположение». Если аргумент опущен, со значения 0,1 (10%).

При расчете ВСД в Excel может возникнуть ошибка #ЧИСЛО!. Почему? Используя метод итераций при расчете, функция находит результат с точностью 0,00001%. Если после 20 попыток не удается получить результат, ВСД вернет значение ошибки.

Когда функция показывает ошибку #ЧИСЛО!, повторите расчет с другим значением аргумента «Предположение».

Примеры функции ВСД в Excel

Расчет внутренней нормы рентабельности рассмотрим на элементарном примере. Имеются следующие входные данные:

Сумма первоначальной инвестиции – 7000. В течение анализируемого периода было еще две инвестиции – 5040 и 10.

Заходим на вкладку «Формулы». В категории «Финансовые» находим функцию ВСД. Заполняем аргументы.

Значения – диапазон с суммами денежных потоков, по которым необходимо рассчитать внутреннюю норму рентабельности. Предположение – опустим.

Искомая IRR (внутренняя норма доходности) анализируемого проекта – значение 0,209040417. Если перевести десятичное выражение величины в проценты, то получим ставку 20,90%.

В нашем примере расчет ВСД произведен для ежегодных потоков. Если нужно найти IRR для ежемесячных потоков сразу за несколько лет, лучше ввести аргумент «Предположение». Программа может не справиться с расчетом за 20 попыток – появится ошибка #ЧИСЛО!.

Еще один показатель эффективности инвестиционного проекта – NPV (чистый дисконтированный доход). NPV и IRR связаны: IRR определяет ставку дисконтирования, при которой NPV = 0 (то есть затраты на проект равны доходам).

Для расчета NPV в Excel применяется функция ЧПС. Чтобы найти внутреннюю ставку доходности графическим методом, нужно построить график изменения NPV. Для этого в формулу расчета NPV будем подставлять разные значения ставок дисконта.

На основании полученных данных построим график изменения NPV.

Пересечение графика с осью Х (когда чистый дисконтированный доход проекта равняется нулю) дает показатель IRR для данного проекта. Графический метод показал результат ВСД, аналогичный найденному в Excel.

Как пользоваться показателем ВСД:

Если значение IRR проекта выше стоимости капитала для предприятия, то данный инвестиционный проект нужно принять.

То есть если ставка кредита меньше внутренней нормы рентабельности, то заемные средства принесут прибыль. Так как в при реализации проекта мы получим больший процент дохода, чем величина капитала.

Вернемся к нашему примеру. Допустим, для запуска проекта брался кредит в банке под 15% годовых. Расчет показал, что внутренняя норма доходности составила 20,9%. На таком проекте можно заработать.

IRR - это Internal Rate of Return, что переводится на русский язык как «внутренняя норма доходности». Так называется один из двух основных методов оценки инвестиционных проектов. В интернете немало статей, представляющих собой краткое изложение данной темы по учебникам финансового анализа. Их общий минус в том, что в них слишком много математики и слишком мало объяснений.

В данной статье приведены не только формула и определение IRR, но есть примеры расчетов этого показателя и интерпретации полученных результатов.

IRR - что это такое? Формула IRR.

IRR или внутренняя норма доходности - это ставка процента, при которой приведенная стоимость всех денежных потоков инвестиционного проекта (т.е. NPV) равна нулю. Это означает, что при такой ставке процента инвестор сможет возместить свою первоначальную инвестицию, но не более того. О том, как пользоваться показателем IRR для одобрения инвестиционных проектов рассказывается чуть дальше в этой статье. Для начала надо научиться рассчитывать величину внутренней нормы доходности IRR, или, как ее еще называют, внутренней нормы рентабельности.

Математика расчета IRR довольно простая. Лучше всего рассмотреть ее на элементарных примерах. Для расчета показателя в одной из более ранних статей на этом сайте были использованы проекты А и Б с одинаковой суммой первоначальной инвестиции (10,000), но с разными по величине притоками денежных средств в последующие 4 года. Удобно будет воспользоваться этими примерами и для изучения формулы расчета показателя IRR.

Приведенная (к сегодняшнему моменту) стоимость всех денежных потоков для четырехлетних проектов будет вычисляться по формуле:

где NPV - чистая приведенная стоимость, CF - денежные потоки (Cash Flows), R - % ставка, стоимость капитала, 0,1,2,3,4 — количество периодов времени от сегодняшнего момента.

Если приравнять NPV к нулю, а вместо CF подставить денежные потоки, соответствующие каждому проекту, то в уравнении останется одна переменная R. Ставка процента, которая будет решением данного уравнения, т.е. при которой сумма всех слагаемых будет равна нулю, и будет называться IRR или внутренней нормой доходности.

Для проекта А уравнение примет вид:

Для проекта Б можно написать аналогичную формулу для расчета IRR, только денежные потоки будут другими:

Чтобы было еще понятнее, можно нанести денежные потоки от проекта на шкалу времени и представить дисконтирование наглядно. Скажем, для проекта А расчет внутренней нормы доходности можно представить в таком виде:

В общем виде для любого инвестиционного проекта формула для расчета IRR выглядит так:

где CF t - денежные потоки от проекта в момент времени t , n — количество периодов времени, IRR - внутренняя норма доходности. Обратите внимание, что понятие IRR в отличие от NPV имеет смысл только для инвестиционного проекта, т.е. когда один из денежных потоков (обычно самый первый) является отрицательным. Этот отрицательный денежный поток и будет являться первоначальной инвестицией. В противном случае мы никогда не получим NPV, равную нулю.

Расчет внутренней нормы доходности с помощью программы Excel — примеры

Вручную с помощью обычного калькулятора найти значение IRR для проектов А и Б невозможно, потому что в данном случае получается уравнение 4-й степени (в нем будет множитель IRR 4 — ставка процента в четвертой степени). Проблему решения такого уравнения n-ой степени можно устранить или с помощью финансового калькулятора, или, что проще, можно воспользоваться встроенной функцией в программе Excel. Эта функция находится в разделе Формулы -> Финансовые, и называется она ВСД (внутренняя ставка доходности).

Для проекта А значение IRR, как видно из рисунка ниже, составит 14,48%.

Чтобы воспользоваться функцией ВСД, в строку «значения» нужно поставить ссылки на ячейки таблицы с суммами денежных потоков. Ячейку «предположение» можно не заполнять, этот аргумент, является необязательным. Выводимое значение 0,144888443 — это и будет искомая IRR, т.е. внутренняя норма доходности данного проекта. Если перевести эту величину в проценты, то она равна 14,48% с точностью до двух знаков после запятой.

Для проекта Б значение IRR согласно Excel равно 11,79%.

Приведу важные пояснения по этой функции из раздела «справка» с моими дополнениями:

Значения должны содержать по крайней мере одну положительную и одну отрицательную величину. В противном случае функция ВСД возвращает значение ошибки #ЧИСЛО!. Действительно, если нет отрицательного денежного потока, то NPV не может быть равно нулю, а в этом случае IRR не существует.
Для расчета функции ВСД важен порядок поступлений денежных средств. Поэтому если потоки денежных средств отличаются по величине в разные периоды, что обычно и бывает, то их необходимо внести в таблицу в соответствии со временем их возникновения.
В Microsoft Excel для вычисления ВСД используется метод итераций. Функцией ВСД выполняются циклические вычисления начиная со значения аргумента «предположение», пока не будет получен результат с точностью 0,00001%. В большинстве случаев для вычислений с помощью функции ВСД нет необходимости задавать аргумент «предположение». Если он опущен, предполагается значение 0,1 (10%).

Другими словами функция ВСД программы Excel будет искать значение IRR подбором, последовательно подставляя в формулу различные величины % ставки, начиная со значения в ячейке «предположение» или с 10%. Если функция ВСД не сможет получить результат после 20 попыток, выдается значение ошибки #ЧИСЛО! Поэтому в некоторых случаях, например, если вы будете считать IRR для ежемесячных потоков за несколько лет, лучше поставить в ячейку «предположение» ожидаемую вами величину ежемесячной процентной ставки. Иначе Excel может не справиться с расчетом за 20 попыток.

Графический метод расчета IRR

До появления персональных компьютеров обычно использовался графический метод определения IRR. Ниже представлены графики изменения NPV для проектов А и Б в зависимости от ставки процента. Для построения графиков нужно найти значение NPV, подставляя в формулу NPV различные значения ставки дисконтирования. можно прочитать в одной из моих предыдущих статей.

На рисунке выше синий график — проект А, красный график — проект Б. Пересечение графиков с осью X (в этой точке NPV проекта равно нулю) как раз и даст значение IRR для этих проектов. Нетрудно видеть, что графический метод дает величину IRR, аналогичную найденным в Excel значениям внутренней нормы доходности для проектов А — 14,5% и Б — 11,8%.

Как пользоваться показателем IRR для оценки инвестиционных проектов?

Любой инвестиционный проект предполагает наличие первоначальной инвестиции (оттока денежных средств), которая приведет к поступлениям денежных средств в будущем (в идеальном случае). Что же показывает внутренняя норма доходности инвестиционного проекта? Она показывает ставку кредита, при которой мы не получим убытка от нашей инвестиции, т.е. результатом всех денежных притоков и оттоков в сумме будет ноль — ни прибыли, ни убытка. В этом случае наша инвестиция в проект окупится будущими поступлениями денежных средств от проекта, но в конечном итоге мы ничего не заработаем.

Правило оценки инвестиционных проектов:

Если величина IRR проекта больше стоимости капитала для компании (т.е. WACC), то проект следует принять.

Другими словами, если ставка кредита меньше ставки инвестирования (внутренней нормы доходности проекта), то заемные деньги принесут добавочную стоимость. Потому что такой инвестиционный проект заработает больший процент дохода, чем стоимость капитала, которая необходима для первоначальной инвестиции.

Например, если вы берете кредит в банке под 14% годовых для того, чтобы вложить средства в бизнес-проект, который принесет вам 20% годовых дохода, то вы на этом проекте заработаете. Если же ваши расчеты окажутся неверны, и внутренняя норма доходности вашего проекта будет ниже 14%, то вам придется отдать банку больше денежных средств, чем вы получите от проекта. То есть вы понесете убыток.

Сам банк поступает точно так же. Он привлекает деньги от населения, скажем, под 10% годовых (ставка по депозиту), а выдает кредиты под 20% годовых (цифра взята «с потолка»). До тех пор, пока ставка по принимаемым банком депозитам будет меньше, чем ставка по выдаваемым банком кредитам, банк будет жить на эту разницу.

Рассчитав показатель IRR, мы узнаем верхний допустимый уровень стоимости заемного капитала, который предполагается инвестировать. Если стоимость капитала (по которой компания может привлечь финансовые ресурсы) выше, чем внутренняя доходность проекта (IRR), то проект принесет убытки. Если стоимость капитала для компании ниже, чем IRR проекта, то компания в каком-то смысле будет работать как банк — жить на разницу между процентными ставками банковского кредитования и рентабельности инвестиции.

Чтобы логика расчета IRR стала еще понятнее, приведу несколько примеров из жизни, с которыми может столкнуться (и сталкивается) обычный человек.

Пример 1 — срочный вклад в Сбербанке

Допустим, у вас есть в наличии 6,000,000 рублей. Прямо сейчас можно сделать срочный вклад в Сбербанк, скажем, на три года. Сумма большая, поэтому нужен самый надежный банк в России. Сбербанк в данный момент предлагает ставку для вкладов свыше 2 млн. рублей на три года в размере 9,0 % годовых без капитализации и 10,29% годовых с ежемесячной капитализацией. Что такое можно прочитать по ссылке.

Поскольку мы будем снимать проценты в конце каждого года, это будет вклад без капитализации процентов, и ставка составит 9% годовых. В конце каждого года можно будет снимать сумму, равную 6,000,000*0,09 = 540,000 рублей. В конце третьего года депозит можно будет закрыть, сняв проценты за третий год и основную сумму в размере 6 миллионов рублей.

Вклад в банке — это тоже инвестиционный проект, поскольку сначала делается первоначальная инвестиция (отрицательный денежный поток), а потом собираются денежные притоки от нашего проекта. Банковский депозит — это финансовый инструмент, и самый простой способ инвестирования, доступный для обычного человека. Раз это инвестиционный проект, то можно рассчитать его внутреннюю норму доходности. Наверное, многие уже догадались, чему она будет равна.

Внутренняя норма доходности (IRR инвестиции) в банковский депозит равна процентной ставке по этому депозиту, т.е. 9%. Если 6,000,000 рублей достались вам в наследство после уплаты налогов, то это означает, что стоимость капитала для вас равна нулю. Поэтому такой инвестиционный проект будет выгоден при любой депозитной ставке. Но взять кредит на 6 миллионов в одном банке и положить эти деньги на депозит в другой банк с прибылью не получится: ставка кредита всегда будет заведомо выше ставки инвестирования. Это принцип работы банковской системы.

Пример 2 — покупка квартиры с целью заработка на сдаче ее в аренду

Свободные денежные средства можно использовать и по-другому, а именно купить квартиру в Москве, сдавать ее в аренду три года, а в конце третьего года продать эту квартиру, чтобы вернуть основной капитал. Денежные потоки от такого проекта будут очень похожи на потоки денежных средств от срочного вклада в банке: примем, что арендная плата для простоты расчета уплачивается арендатором квартиры сразу за год в конце каждого года, а стоимость квартиры в рублях через три года останется такой же, как и сейчас. Я намеренно упрощаю ситуацию, более сложные расчеты вы сможете сделать самостоятельно.

Я выбрала в Интернете первую же попавшуюся квартиру за 6 млн. рублей на СЗ Москвы. Аренда подобной однокомнатной квартиры стоит 30,000 рублей в месяц. Налоговые последствия данных сделок для простоты не учитываются.

Итак, арендная плата за год составит 30,000*12 = 360,000 рублей. Чтобы было нагляднее, денежные потоки от обоих проектов — вклад в Сбербанке и сдача 1-комнатной квартиры в аренду на северо-западе Москвы — показаны вместе в таблице ниже:

Даже без вычисления IRR видно, что сейчас банковский депозит является более доходным вариантом. Легко доказать это, если рассчитать внутреннюю норму доходности для второго проекта — она будет ниже, чем IRR по депозиту. При сдаче данной однокомнатной московской квартиры в течение трех лет при условии ее продажи в конце третьего года IRR инвестиции составит 6,0% годовых.

Если у вас нет наследства в сумме 6 млн рублей, то брать эти деньги в кредит, чтобы сдавать квартиру в аренду неразумно, так как ставка кредитования сейчас заведомо выше, чем 6,0% внутренней доходности данного проекта. Причем IRR не зависит от количества лет сдачи квартиры в аренду — внутренняя норма доходности останется такой же, если вместо трех лет сдавать ее в аренду 10 лет или 15.

Если учесть ежегодное подорожание квартиры в результате инфляции, IRR данного проекта будет выше, Например, если в первый год (2015) рублевая стоимость квартиры вырастет на 10%, во второй (2016) на 9%, а в третий (2017) на 8%, то к концу третьего года ее можно будет продать за 6,000,000*1,10*1,09*1,08 = 7,769,520 рублей. Такое увеличение денежного потока в третий год проекта даст IRR, равную 14,53%. Поэтому если бы мы могли предсказать будущие рублевые цены на квартиры с большой точностью, то наш проект стал бы более реальным. Но все равно невыгодным в нынешней ситуации, когда ставка рефинансирования ЦБ равна 17%, и, соответственно, все банковские кредиты слишком дороги.

Расчет IRR при ежемесячных потоках денежных средств

С помощью функции ВСД можно рассчитать IRR инвестиционного проекта при равных промежутках времени между денежными потоками. Результатом вычислений будет процентная ставка за период — год, квартал, месяц. Например, если бы мы считали, что платежи за аренду квартиры приходят в конце каждого месяца (а не года), то надо было бы сделать таблицу Excel с 36-ю платежами по 30,000 рублей. В этом случае функция ВСД выдала бы значение внутренней нормы доходности проекта за месяц . Для нашего проекта IRR получилась равной 0,5% в месяц. Это соответствует годовой % ставке в размере 6,17% (рассчитывается как (1+0,005) 12 -1), что ненамного больше, чем 6,0%, рассчитанных ранее.

Если вы захотите получить этот результат самостоятельно, обязательно заполните ячейку «предположение» — поставьте туда 0,03, иначе вы получите на выходе ошибку #ЧИСЛО!, потому что Excel не хватит 20 попыток, чтобы рассчитать IRR.

Расчет IRR при неравных промежутках времени между денежными потоками

Excel предоставляет возможность рассчитать внутреннюю норму доходности проекта и в том случае, если денежные потоки от проекта поступают через неравные промежутки времени. Для расчета IRR такого проекта надо использовать функцию ЧИСТВНДОХ и в качестве аргумента указать не только ячейки с денежными потоками, но и ячейки с датами их поступлений. Например, если мы перенесем срок продажи квартиры вместе с последней арендной платой на конец четвертого года (с 31.12.17 на 31.12.18), а в конце третьего года у нас не будет поступлений денежных средств, то IRR упадет с 6% до 4,53% годовых. Обратите внимание, что рассчитать внутреннюю норму доходности в данном случае можно будет только с помощью функции ЧИСТВНДОХ, потому что фукция ВСД даст тот же результат, который и был — 6%, т.е. изменение периода времени ВСД не учтет.

«Куда идем мы с Пятачком, большой, большой секрет…»

Нынешняя ставка рефинансирования, равная 17%, убивает и бизнес, и банки. Потому что трудно найти инвестиционные проекты, которые бы окупались при таких ставках кредитования. Как развивать бизнес в подобных условиях? Торговля оружием и наркотиками, конечно, будут прибыльны и в этом случае, но большая часть бизнесов будут в лучшем случае выживать, а в худшем разорятся.

И как будут зарабатывать банки, если инвестиционных проектов с такой высокой доходностью просто не существует? А чтобы платить нам выросшие проценты по вкладам, банки должны где-то зарабатывать средства для этого.

Россия смогла бы выдержать и более низкий курс рубля по отношению к основным валютам, но справиться еще и с высокой процентной ставкой в экономике — это уже перебор.

В 2014 году мы неоднократно слышали, что ЦБ РФ занимается таргетированием инфляции. И делалось это с благими намерениями — чем ниже инфляция, тем легче добиться окупаемости инвестиций. Но получается, что хотели «как лучше», а получилось «как всегда». При дорогой валюте, как сейчас, в России могло бы успешно развиваться собственное производство, импортозамещение стало бы реальностью. Но нет, мы не ищем легких путей, а что хуже всего, мы не учимся на своих ошибках. И живем, как в том анекдоте:

«В прошлом году посеяли 100 га пшеницы. Все поел хомяк…В этом году собираемся засеять 200 га пшеницы. Нехай хомяк подавится!»

Инвестирование – один из интересных способов заработка средств, который заключается в покупке выгодных (по мнению инвестора) активов перспективных компаний и проектов. В мире, который построен на современных рыночных (капиталистических) правилах игры, именно этот процесс является одной из его двигающих сил.

Но как определить, что тот или иной проект действительно выгоден и принесет доход? Стопроцентной гарантии никто никогда дать не может – это обратная сторона медали такого способа заработка. Тем не менее, расчет рисков для той или иной ценной бумаги (или облигации) возможно легко произвести вычисление, что минимизирует вероятность невыгодной покупки.

Дорогие читатели! Статья рассказывает о типовых способах решения юридических вопросов, но каждый случай индивидуален. Если вы хотите узнать, как решить именно Вашу проблему - обращайтесь к консультанту:

ЗАЯВКИ И ЗВОНКИ ПРИНИМАЮТСЯ КРУГЛОСУТОЧНО и БЕЗ ВЫХОДНЫХ ДНЕЙ .

Это быстро и БЕСПЛАТНО !

Именно для этих целей и была создана формула расчета ВНД (англ. IRR – «Internal rate of return»). Она включает в себя ключевые финансовые показатели акции или ценной бумаги и является действительно удобным способом рассчитать убыточность (или доходность).

Оценка рисков таким образом является простой и доступной даже тем, кто не слишком знаком с математическим анализом и экономикой, а полученный коэффициент легко анализируется и читается. Как итог: при знании нюансов и соблюдении ряда правил получаем работающий метод для оценки рисков при инвестировании.

Определение понятия и цели расчета IRR

Внутренняя норма доходности (ВНД или IRR) – ключевой критерий анализа любого доступного для инвестирования проекта. Фактически, эта величина позволяет определить минимальную ставку дисконта, при которой дисконтированные доходы от акции, опциона или ценной бумаги находятся в состоянии равенства с суммой вложения.

Фактически, определение ВНД базируется на уравнении, в котором чистая текущая стоимость (рентабельность) является нулевой. При поиске информации об IRR часто можно наткнуться на схожие термины и его варианты: внутренняя норма доходности, внутренняя ставка доходности, внутренняя ставка отдачи, норма рентабельности или норма возврата инвестиций. Проблемы с адаптацией термина привели даже к ряду сложностей при поиске информации о расчетах.

Уравнение ВНД отражает ту ситуацию, когда инвестиционный проект отдает вложившему в него средства не только инвестиционных средств, но и первоначальных вложений в ценные бумаги. Фактически, в нем рассматривается случай, когда соотношение вложенных средств к доходу является равным. Если финансовые показатели проекта приводят инвестора к каноничному уравнению IRR – это значит, что проект принесет столько же денег, сколько на него было потрачено.

Что можно получить от расчета ВНД? Ответ на вопрос о целесообразности вложений куда-либо. Фактически, уравнение позволяет узнать, какой объем вложенных средств сможет вывести проект «в ноль» и не сделать его убыточным. Подгоняя показатели под каноничную форму уравнения, инвестор может легко сравнить значение необходимого капитала с реально доступным ему и принять решение о вложении или отказе от него.

Подобранная ставка, увеличивающая денежный поток, дает возможность прийти к состоянию равновесия в расчетах. Если полученный таким образом показатель ВНД выше ставки прибыли за вложенные средства – инвестиция может быть произведена. Если ниже – проект однозначно не стоит инвестиций.

Формула расчета инвестиционного проекта

Внутренняя норма доходности рассчитывается по следующей формуле:

Другой вид формулы (с теми же обозначениями) выглядит так:

Расчет в Excel

Найти полследовательность арифметических действий, позволяющую вычислять ВНД в Microsoft Office Excel, не представляется возможным. Причина в том, что для полноценного вычисления показателей программой ей придется составить и решить уравнение четвертого порядка – такими функциями данный софт не обладает.

Благо, есть более простой способ: Excel обладает колоссальным запасом встроенных функций, среди которых нашлось место и ВСД (внутренняя ставка доходности). Достаточно лишь пройти в подменю «Финансовые» основной вкладки «Формулы» и выбрать соответствующий пункт в выпадающем списке.

Затем выстраиваем в один из столбцов доходность инвестиции, выделяем их (или прописываем в меню «Значения» при добавлении функции). Результат можно увидеть либо во всплывающем окне (графа «Значение» внизу), либо вывести ее на отдельную ячейку и изменять показатели, просчитывая каждое условие отдельно.

Ответ будет получен при определенных условиях:

когда в перечне данных имеется хотя бы одно отрицательное число (при отсутствии отрицательного денежного потока IRR даже теоретически не может равняться 0);
при правильном порядке указания поступлений (сначала первый год (месяц, квартал), потом второй, третий и так далее);
если не введены данные в поле «Предположение» – это может повлиять на вычисление, производимое методом итераций (подбора).

Графический метод определения ВНД

Основное преимущество использования графического метода заключается в наглядности и простоте: достаточно просто построить таблицу и на ее основании (на компьютере или даже вручную) создать график зависимости.

В таблицу необходимо внести периоды, а также данные по денежным потокам проекта (или даже нескольких). Наиболее удобно делать это в том же табличном процессоре Excel. Дисконтировать по разным процентным ставкам (например, 5, 10 и 15%) и затем подобрать показатель более точно можно по приведенному в статье аналитическому алгоритму.

Далее на простроенных графиках ищем нулевую ось (где NPV = 0) и смотрим, какой ставке соответствует проект. Большой плюс метода – возможность наглядно сравнить инвестиционный потенциал сразу нескольких опций одновременно.

Практическое применение коэффициента

Любая инвестиция предполагает расставание с определенной суммой денежных средств, которые в теории должны дать уже прибыль (положительную разницу дохода с расходом). Показатель IRR дает ценную информацию: кредитную ставку, при которой инвестиция не окажется убыточной. При составлении уравнения определяются условия, когда проект не будет ни прибыльным, ни убыточным.

Далее все предельно просто: в случае, если показатель ВНД больше, чем общая итоговая цена капитала – проект стоит рассмотреть для инвестирования. Если нет – он даже теоретически не может быть рентабельным: в таком случае взятые в заем (кредит) средства смогут дать добавочную стоимость при вложении.

Именно по такой схеме и работают банки, проводя операции только с положительным IRR: достаточно сравнить ставки по депозитам (не более 15%) со процентами по выдаваемым в долг деньгам (не менее 20%). Разница же и составит прибыль от деятельности банка (в нашем случае), да и любого инвестиционного проекта в целом. Именно ВНД дает понять, каков максимальный порог возможного займа, который можно вложить в ценные бумаги, компанию и так далее.

Примеры

Пример первый – простейшие практические расчеты при имеющихся базовых показателях. Расчет нормы доходности при неизменной барьерной ставке. Объем вложенных средств равняется 30000$.

Доходы:

Период 1	10000$
Период 2	12000$
Период 3	11000$
Период 4	10500$

Показатель эффективной барьерной ставки — 10%.

Можно произвести вычисления без привлечения софта. Берем стандартный способ подходящего приближения, который часто используется в таких случаях.

Подбираем барьерные ставки приближенно, дабы «окружить» минимальные абсолютные значения NPV, и после осуществляем приближение. Этот метод подразумевает несколько расчетов IRR.

В крайних ситуациях можно построить функцию NPV(r)), но об этом – в разделе ниже.

Произведем вычисления барьерной ставки для r a =10,0%.

Теперь пересчитаем денежные потоки в виде нынешних стоимостей:

За первый период	PV 1 = 10000 / (1 + 0,1)^1 = 9090
За второй период	PV 2 = 12000 / (1 + 0,1)^2 = 9917
За третий	PV 3 = 11000 / (1 + 0,1)^3 = 8264
За четвертый	PV 4 = 10500 / (1 + 0,1)^4 = 7171

Итого, чистая текущая стоимость при ставке 10% (или 0,1) составляет:

NPV = (9090 + 9917 + 8264 + 7171) — 40000 = 4442$.

Теперь попробуем сделать то же, но для ставки в 15%.

Пересчитаем денежные потоки в образ нынешних стоимостей:

PV 1 = 10000 / (1 + 0,15)^1 = 8695;
PV 2 = 12000 / (1 + 0,15)^2 = 9073;
PV 3 = 11000 / (1 + 0,15)^3 = 7232;
PV 4 = 10500 / (1 + 0,15)^4 = 6003.

Для этой процентной ставки NPV вычисляется аналогично:

NPV = (8685 + 9073 + 7232+6003) — 35000 = — 4007$

Используем формулу приближения и получаем процент:

IRR = r a + (r b — r a) * NPV a /(NPV a — NPV b) = 10 + (15 — 10)*4442 / (4442 — (- 4007)) = 12,6%

Равенство справедливо, если r a < IRR < r b и NPV a > 0 > NPV b .

Ответ: полученный показатель окупаемости инвестиции составляет 12,6%, что выше заданной вначале эффективной барьерной ставки в 10%. Вывод: проект достоин рассмотрения и может стать рентабельным.

Тем не менее, подобный алгоритм не работает в тех случаях, когда внутреннюю норму доходности необходимо находить при изменяющейся барьерной ставке.

Дано:

Условие то же, что и в прошлом примере: вычислить вероятность окупаемости проекта и целесообразность инвестирования в него. Рассчитаем для ставки дисконтирования одинаковой r a =20,0%

Подсчитываем внутреннюю норму, как и в предыдущем примере:

NPV = (6666 + 4513 + 4050) — 15000 = 229$

Теперь сделаем те же вычисления для r b = 25,0%

Пересчитаем денежные потоки в вид текущих стоимостей:

Первый отрезок времени	PV 1 = 8000 / (1 + 0,25)^1 = 6400$
Второй отрезок времени	PV 2 = 6500 / (1 + 0,25)^2 = 4160$
Третий отрезок времени	PV 3 = 7000 / (1 + 0,25)^3 = 3584$

И все та же норма по аналогии:

NPV = (6400 + 4160 + 3584) — 15000 = — 864$

Итоговый показатель составит:

IRR = 20 + (25 — 20)*229 / (229 — (- 864)) = 21%

Так как показатель барьерной ставки изменяется, то сопоставление необходимо сделать именно с показателем внутренней барьерной ставки. В соответствии с расчетом образца эффективная барьерная ставка составит 10,895%. Вывод таков: полученный окупаемости равен 21%, что значительно выше имеющихся средних 11%. Можно смело инвестировать в проект.

Ценное замечание: правило, согласно которому выбирается проект с большим показателем внутренней нормы доходности, действует лишь в общих случаях. Оценка может изменяться кардинально, если учесть реинвестиции. В таком случае показателя барьерной ставки недостаточно проект с меньшим IRR, может быть выгоднее проекта с большими цифрами.

Модифицированная ВНД (MIRR)

Как уже говорилось выше, ВНД учитывает лишь те ситуации, в которых осуществляется первичное инвестирование. В случаях, когда происходит повторное вложение средств, он не работает: полученные по расчетам результаты могут прямо противоречить целесообразности вложения средств. Для облегчения задачи именно в этих ситуациях была создана модифицированная ВНД (или MIRR).

Формула для ее определения выглядит подобным образом, только учитывает ставку реинвестирования:

К слову, в Excel имеется и эта функция – она находится в том же списке под названием «МВСД».

Недостатки использование данного метода

Существует ряд существенных недостатков, которые могут оттолкнуть инвестора от использования вычислений на базе IRR:

относительная громоздкость расчетов в случае большого количества отрезков времени;
необходимость получения полных и актуальных данных о движении капитала в предприятии – чистая прибыль может отличаться от имеющейся в расчетах;
графический способ позволяет визуально оценить необходимую величину процентной ставки, но дает лишь приблизительные результаты.

Ограничения и недостатки внутренней нормы доходности

Существует сразу несколько ограничений, которые накладывает на инвестора использование ВНД или МВНД:

трудно прогнозировать движение денежных средств в будущем – многие факторы формула попросту не учитывает;
с помощью IRR и MIRR не представляется возможным вычислить дисконтированный объем средств для вложения;
если брать за основу разные периоды или иметь дело с произвольным чередованием прибыли и убытков – можно получить сразу несколько отличных друг от друга показателей ВНД, что способно запутать при принятии решения;
стандартная формула ВНД никак не может описать процесс реинвестирования и способна выдавать в этом случае прямо противоречащие реальному положению дел результаты.

ВНД (или IRR) – один из значимых экономических показателей, который подойдет для предварительной оценки потенциала определенного вложения. Метод имеет как преимущества, так и недостатки, но все же среди простых и доступных достоит занять свое заслуженное место. Ключевой плюс – возможность выполнить расчеты четырьмя разными способами (аналитически, графически и посредством табличного процессора).